Question

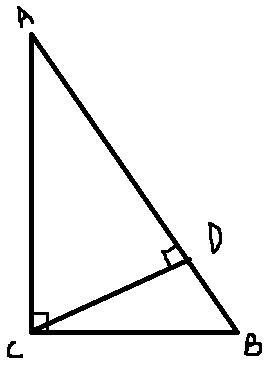
На сторонах прямого угла С взяты точки
А и В. Из точки С опущен перпендикуляр
CD на прямую АВ. Докажите
равенство углов ACD и ABC.

Answer 1

Ответ:

Объяснение:

Рассмотрим прямоугольные тр-ки △ABC и △ACD. У них один угол общий <CAB=<CAD, а углы <ACB=<ADC=90°. Значит тр-ки подобны и у них равны оставшиеся соответствующие углы <ABC=<ACD чтд.

Хотя и без подобия тр-ков очевидно, что оставшиеся соответствующие углы равны, так как сумма углов треугольника равна 180, а все прочие углы попарно равны.