Предмет: Геометрия,
автор: zarinasharshanlo
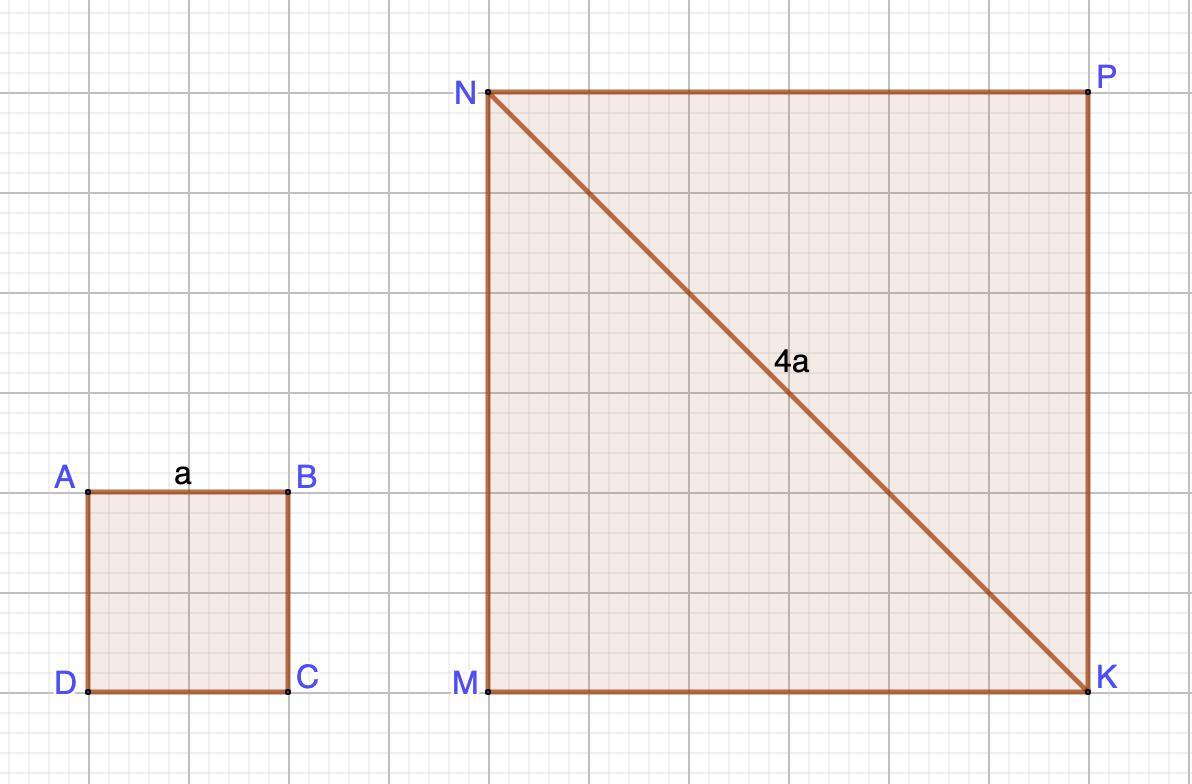
Периметр квадрата ABCD равен длине диагонали квадрата MNPK. Найди отношение площадей двух этих квадратов.
Fayneyp:
1 / 8
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Дано: ABCD - квадрат;
MNPK - квадрат;
- диагональ MNPK.
Найти:
Решение.
Пусть сторона квадрата ABCD равна а.
- Периметр - сумма всех сторон.
Стороны квадрата равны.
⇒
Значит NK = 4a.
Найдем площади квадратов по формулам:
,
где а - сторона квадрата, d - диагональ квадрата.
⇒
Найдем отношение площадей:
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: rasyla008
Предмет: Русский язык,
автор: konokindanya
Предмет: Математика,
автор: МиЛаФфКо
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ymnik341