Предмет: Алгебра,
автор: Jasper271
Здравствуйте! Нужна срочная помощь!
Приложения:
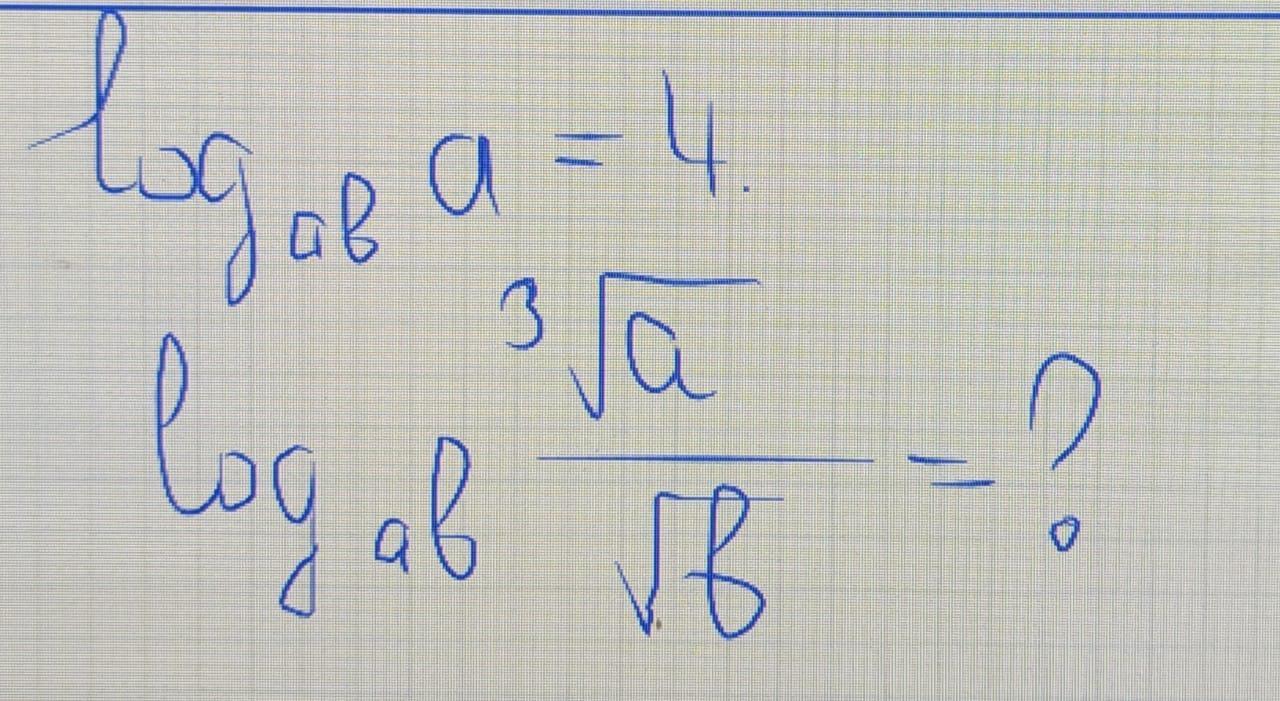
Ответы
Автор ответа:
0
Ответ:
Jasper271:
Спасибо тебе большое! У меня были сомнения, но все совпало! Спасибо еще раз!
хорошо, потому что у меня тоже были сомнения))
у меня в первый раз получилось 15/6 я минус забыла
Похожие вопросы
Предмет: Алгебра,
автор: KateIlyxa359
Предмет: Математика,
автор: 1984roksana
Предмет: Геометрия,
автор: itsannmirr
Предмет: Математика,
автор: 26031970nata1
Предмет: Литература,
автор: nastyaharisova