Коло вписане в рівнобічну трапецію, ділить точкою дотику бічну сторону на відрізки завдовжки 8см і 18 см. Знайдітьоснови трапеції і радіус вписаного кола
Ответы
Ответ:
R =12, АD=36см, ВС=16см
Объяснение:
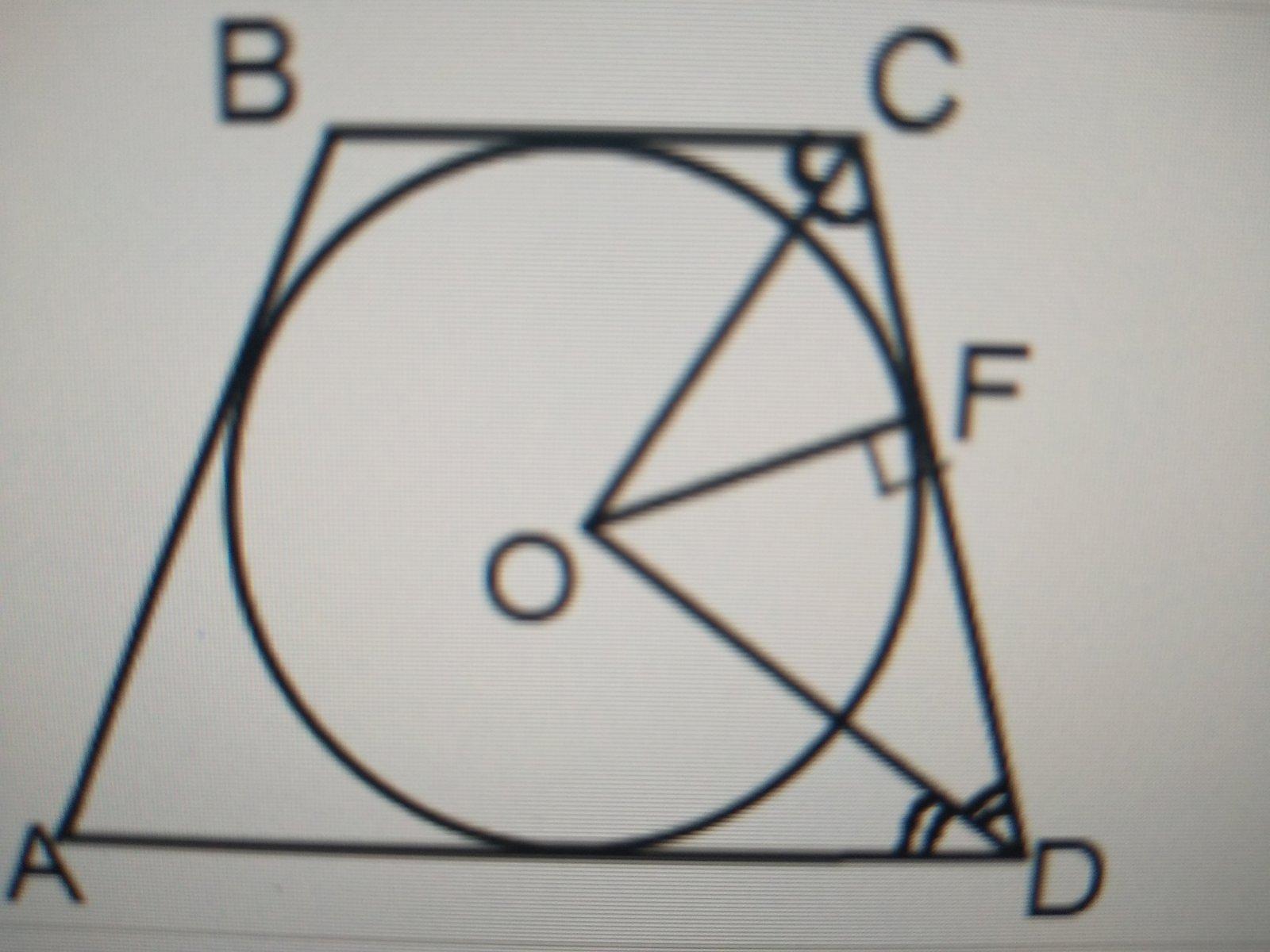
1) ∠ADC + ∠BCD = 180º (як сума внутрішніх односторонніх кутів при паралельних прямих AD і BC і січною CD);
2) так як точка O - точка перетину биссектрис кутів трапеції, то ∠ODF + ∠OCF = 1/2 ∙ (∠ADC + ∠BCD) = 90º;
3) так як сума кутів трикутника дорівнює 180º, то в трикутнику COD ∠COD = 90º;
4) таким чином, трикутник COD прямокутний, а OF - висота, проведена до гіпотенузи, CF і FD - проекції катета OC і OD на гіпотенузу. Оскільки висота, проведена до гіпотенузи, є середнім пропорційним між проекціями катетів на гіпотенузу, то OF =√CF *FD ; OF= R вписаного кола. R =√m*n R =√8*18=√144=12см
5)Знайдемо бічні сторони трапеції, враховуючи, що в чотирикутник можна вписати коло тоді і тільки тоді, коли суми довжин його протилежних сторін рівні. Звідси випливає, що якщо в трапецію вписане коло, то сума її основ дорівнює сумі бічних сторін:
Сума бічних сторін=2(8+18)=52см. Сума основ=52 см
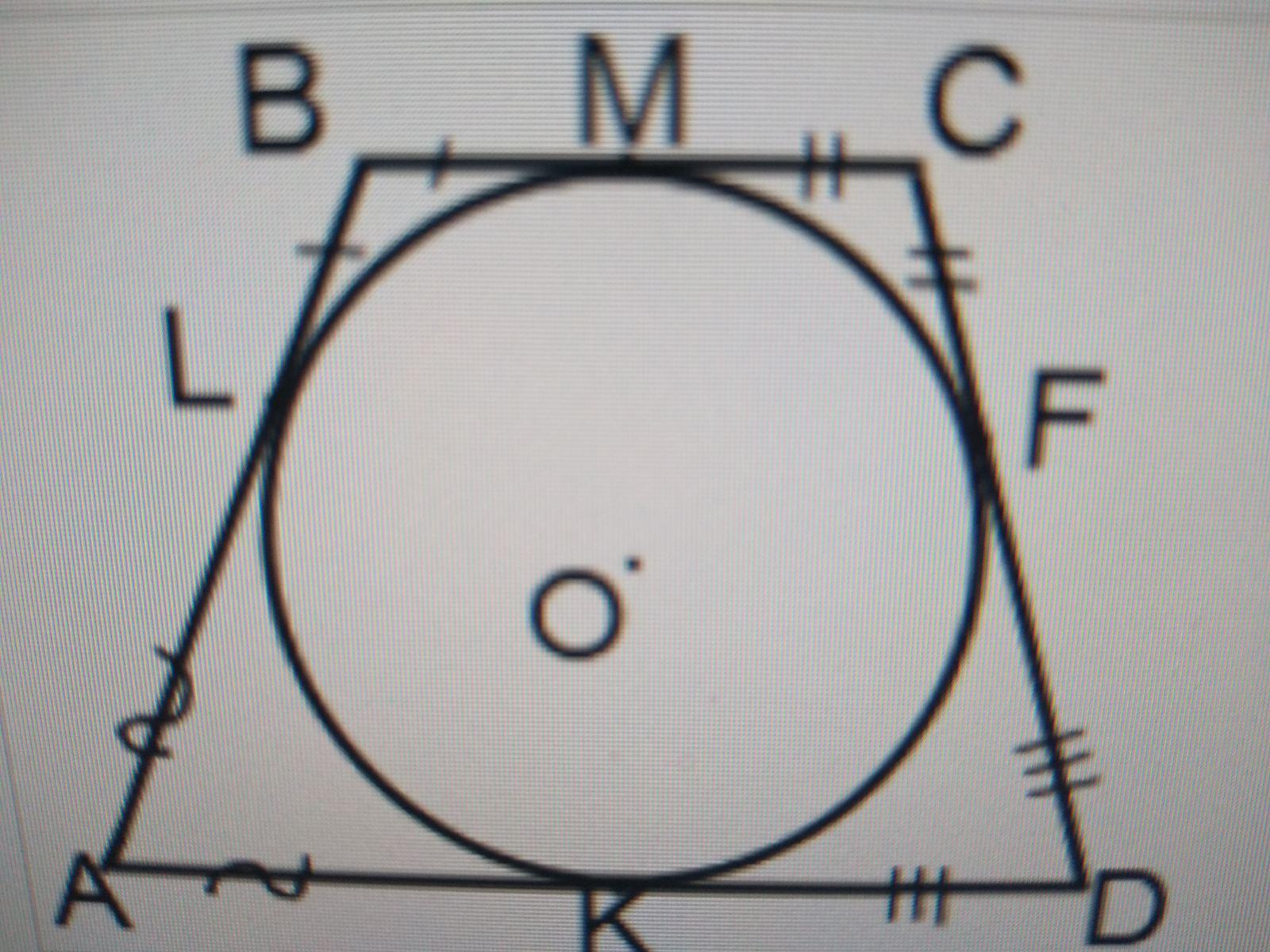
Відрізки дотичних, проведених з однієї точки, рівні. Звідси слідує, що
AL=AK, BL=BM,, CM=CF, DF=DK.
Отже: ВС=BM+CM=8+8=16 см, а АD=AK+KD=18+18=36см.