Предмет: Математика,
автор: oleg222538
Вычислить производную dy/dx функций
Приложения:
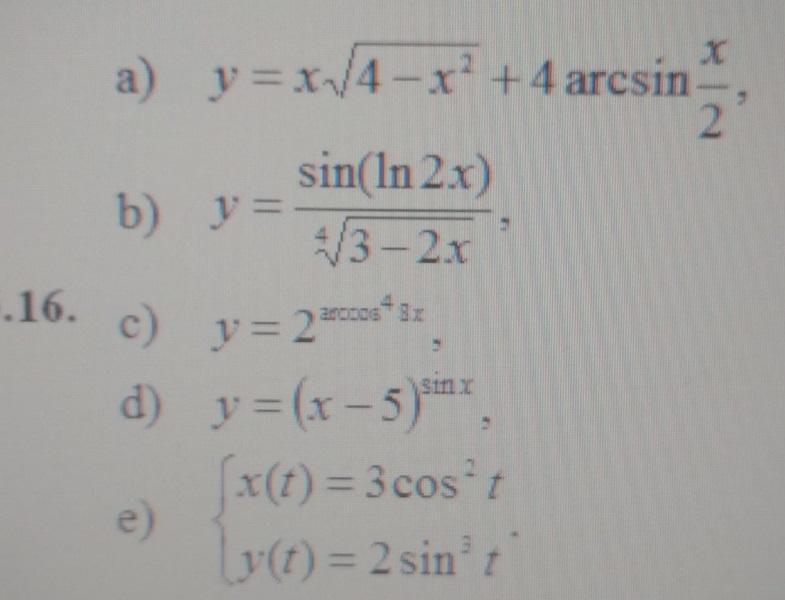
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
г)
д)
Похожие вопросы
Предмет: Математика,
автор: Таня1210
Предмет: Математика,
автор: vityapatskevich
Предмет: Обществознание,
автор: Dashka161
Предмет: Химия,
автор: Makka98
Предмет: Литература,
автор: vikasS0S