Предмет: Математика,
автор: faceit033
100 баллов,найти интеграл
Приложения:
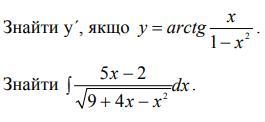
Ответы
Автор ответа:
1
1.
2.
в числителе делаем производную знаменателя:
первый интеграл:
второй интеграл:
выделяем квадрат суммы/разности в знаменателе:
Ответ:
EmilyFortlander:
Здраствуйте!
Можете помочь мне с Алгеброй?
Похожие вопросы
Предмет: Математика,
автор: Зайчишка00
Предмет: Биология,
автор: ospanovstep
Предмет: Русский язык,
автор: arutyunov
Предмет: Химия,
автор: paveltatarniko
Предмет: Математика,
автор: oyulik1