Предмет: Математика,
автор: serator37
Найти производную функции
y=sqrt(arcctg(x/2))
Приложения:
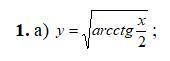
Ответы
Автор ответа:
1
Ответ:
ptimofej397:
здравствуйте, помогите пожалуйста, задание в профиле, очень прошу вас
Похожие вопросы
Предмет: Алгебра,
автор: polinazorina2
Предмет: Математика,
автор: buny201251
Предмет: Английский язык,
автор: faleeva791
Предмет: Математика,
автор: Нуржан2612006
Предмет: Математика,
автор: Polina0915