Предмет: Алгебра,
автор: ria2015
В квадрат, сторона которого равна 76 см, вписан другой квадрат, вершины которого серединами сторон первого квадрата, в этот квадрат вписан, так же, другой квадрат, и т.д.
Сторона третьего квадрата= ?
Ответы
Автор ответа:
0
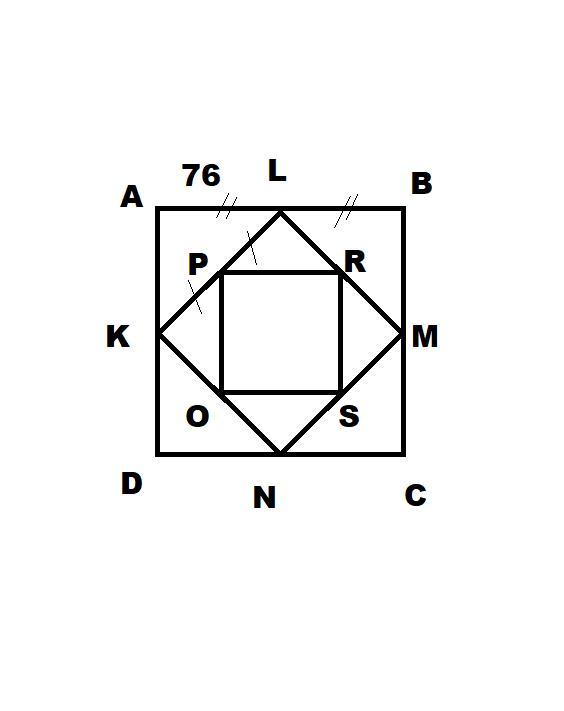
Дано квадрат АВСD со стороной 76 см, в который вписан другой квадрат, KLMN, вершины которого делят стороны первого квадрата пополам.
AL=BL=76/2=38 см.
Имеем прямоугольный равнобедренный треугольник ALK, где ∠А=90°
Исходя из теоремы Пифагора, KL=√(AL²+AK²)
KL=√(38²+38²)= √(2*38²)=38√2 см
В квадрат KLMN со стороной 38√2 см, в который вписан квадрат OPRS, вершины которого делят стороны вышеуказанного квадрата пополам.
KP=PL=38√2 / 2=19√2 см.
Имеем прямоугольный равнобедренный треугольник КРО, где ∠К=90°
Исходя из теоремы Пифагора, РО=√(КР²+КО²)
РО=√((19√2)²+(19√2)²)=√(722+722)=√1444=38 см
Ответ: сторона третьего квадрата 38 см.
Приложения:
ria2015:
Спасибо за подробный ответ:))
Пожалуйста)
Похожие вопросы
Предмет: Математика,
автор: М2А0Ш0Ф3
Предмет: Литература,
автор: dimagherghi20
Предмет: Русский язык,
автор: YDanil
Предмет: Химия,
автор: Fischerry