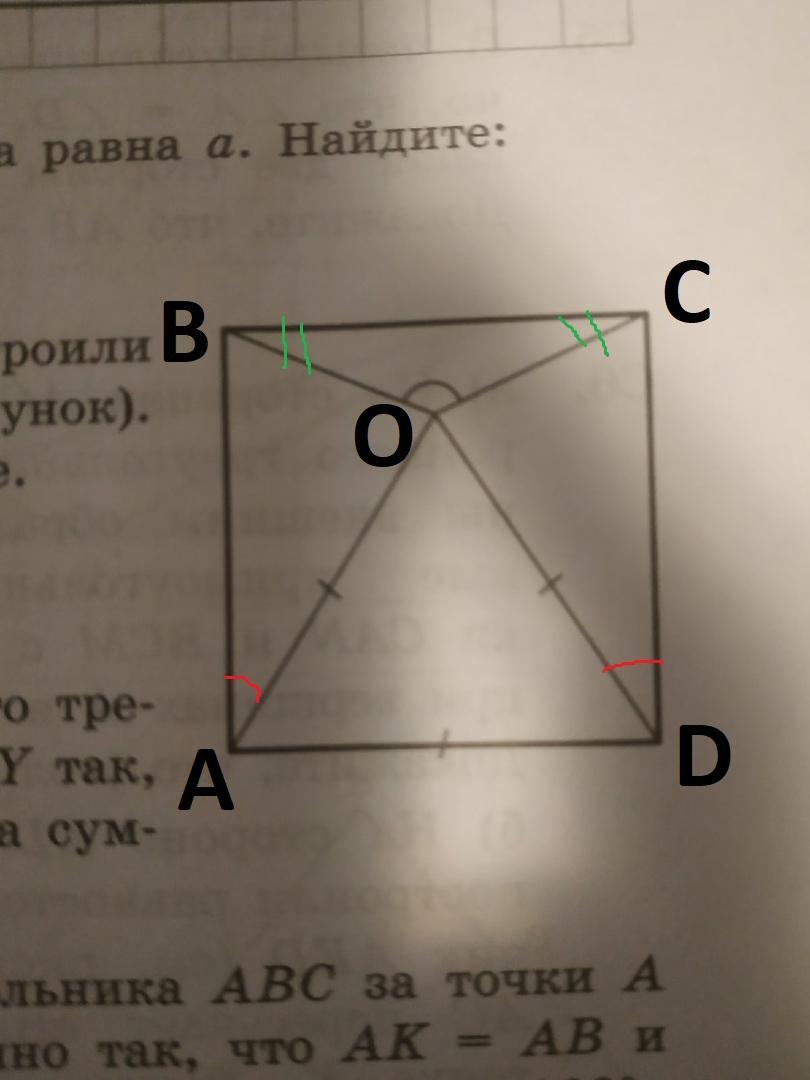
На стороне квадрата внутри его построили равносторонний треугольник Найди угол, отмеченный на рисунке.
Ответы
Ответ:
150°
Объяснение:
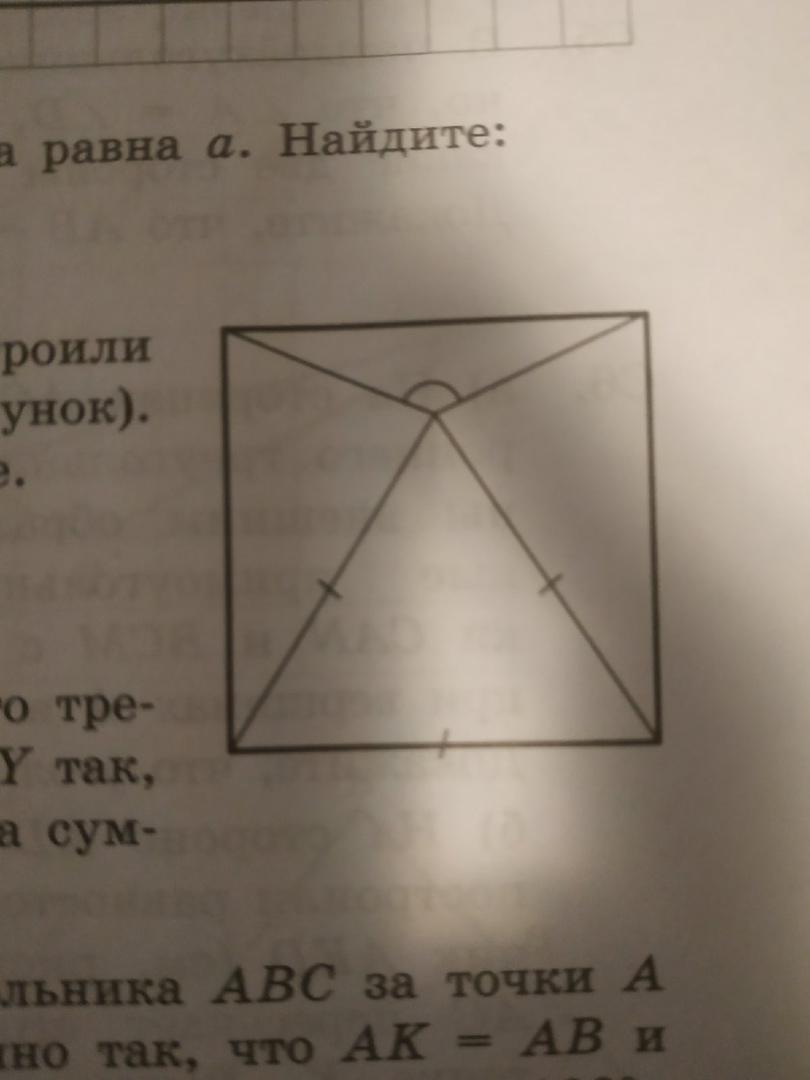
Смотрите рисунок!
Пусть вершины квадрата ABCD и точка O вершина правильного треугольника(ΔAOD) (смотрите рисунок).
AB = BC = CD = DA = AO = OD, так как все стороны квадрата равны, а одна из сторон квадрата является стороной правильного треугольника.
По свойствам правильного треугольника все его углы 60°.
∠BAO = ∠CDO = 90° - 60° = 30°. Треугольник ΔBAO = ΔCDO по первому признаку равенства треугольников так как ∠BAO = ∠CDO = 30°, а
AO = OD = AB = CD. Так как ΔBAO - равнобедренный (AB = AO), то углы при основании равны, тогда ∠BOA = (180° - ∠BAO)0,5 =
= (180° - 30°)0,5 = 75°. Так как ΔBAO = ΔCDO, то соответствующие углы равны, тогда ∠BOA = ∠COD = 75°.
∠BOC + ∠BOA + ∠COD + ∠AOD = 360°
∠BOC = 360° - (∠BOA + ∠COD + ∠AOD) = 360° - (75° + 75° + 60°) =
= 360° - 210° = 150°.