Предмет: Математика,
автор: vladmops6
Помогите пожалуйста!!!!
Приложения:
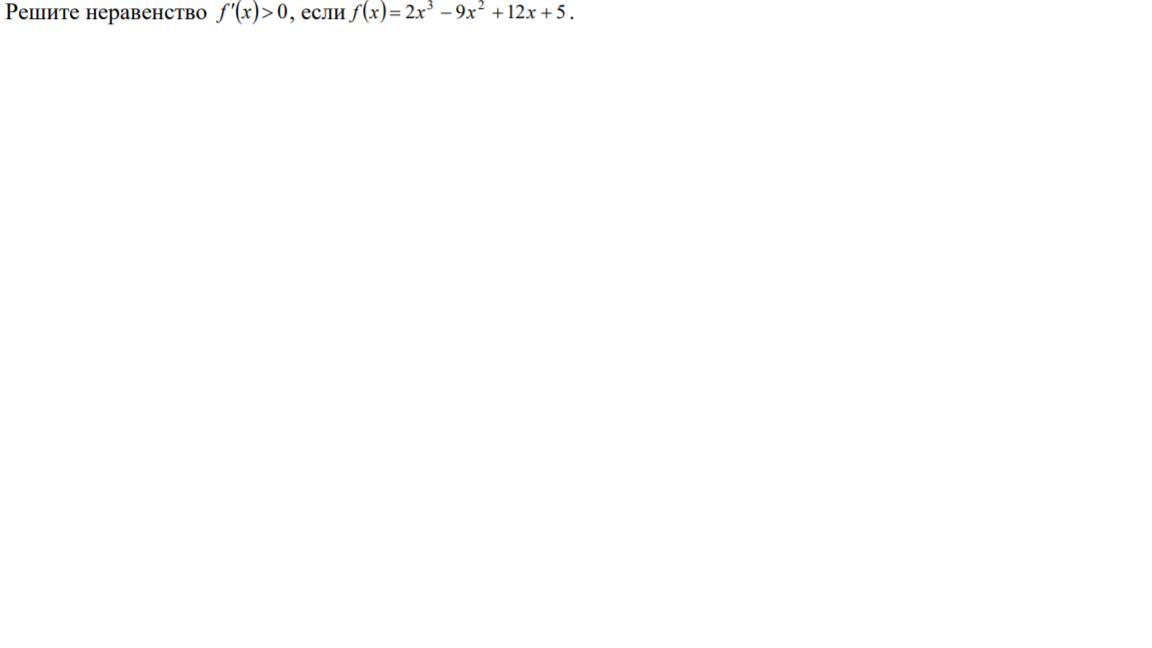
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Нули функции:
Определим знаки неравенства на интервалах
Неравенство принимает положительные значения на интервалах
значит,
Похожие вопросы
Предмет: Математика,
автор: ипптри
Предмет: Биология,
автор: arinashal
Предмет: Математика,
автор: hamedova
Предмет: Математика,
автор: 16Sonybobr16
Предмет: Математика,
автор: vik115