Question

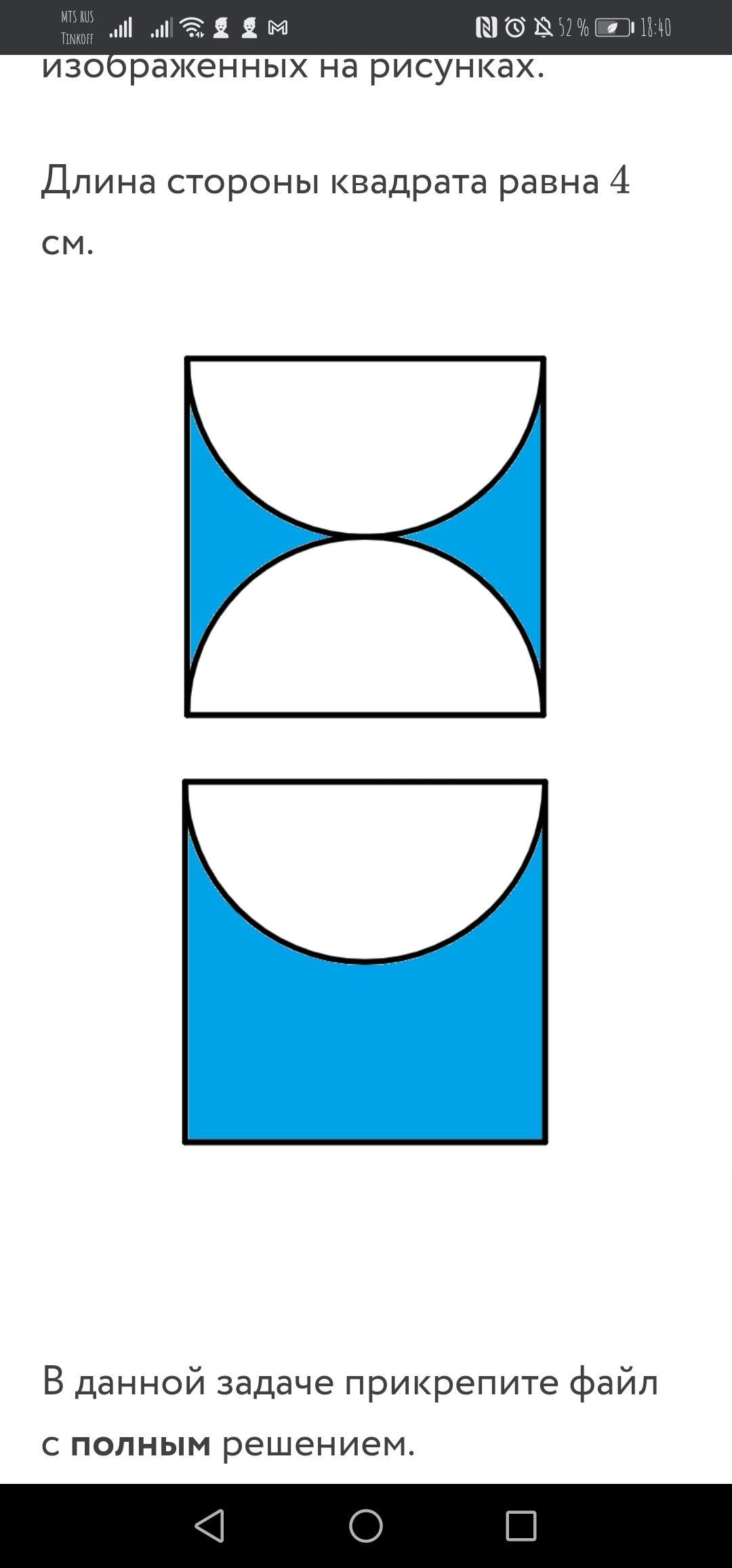
Вычислите площади закрашенных голубым цветом фигур, изображённых на рисунках.

Длина стороны квадрата равна 4 см.

Answer 1

Зная длину стороны квадрата, можно найти его площадь: $S_{\Box} = a^2 = 4^2 = 16$ см².

1) В этом квадрате проведены два полукруга. Мысленно доведём их до полных кругов. У каждого из них диаметр равен стороне квадрата, то есть, 4 см. Радиус же равен половине диаметра, то есть, $R = \dfrac{d}{2} = \dfrac{4}{2} = 2\ _{CM}$ . Площадь полукруга равна половине площади полного круга, получаем  $S = \dfrac{\pi R^2}{2} = \dfrac{3,14\cdot 2^2}{2} = 3,14\cdot 2 = \bf{6,28}\ _{CM^2}$ . Таких полукругов в квадрате два. Чтобы найти площадь закрашенной голубым части, нужно из площади квадрата вычесть площади этих полукругов:  $S_x = 16 - 6,28 - 6,28 = 16 - 12,56 = \boxed{\bf{3,44}}$ см².

2) Всё то же самое, но полукруг уже один. Все данные мы вычислили в прошлом пункте и можем сразу найти искомую площадь:  $S_x = 16 - 6,28 = \boxed{\bf{9,72}}$ см².