Question

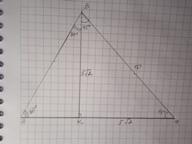
Высота BK треугольника ABC делит сторону AC на отрезки BK,CK. BC - 10 см, угол A=60°, угол CBK=45° Найдите отрезок AK - ?

Answer 1

Ответ:

(5√6)/3 cм

Объяснение:

Дано: ΔАВС,  ВК - высота,  ВС=10 см,  ∠А=60°,  ∠СВК=45°. Найти АК.

Рассмотрим ΔКВС - прямоугольный,  ∠КВС=∠С=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°, значит ВК=КС.

Пусть ВК=КС=х см,  тогда по теореме Пифагора

10²=х²+х²;  2х²=100;  х²=50;  х=√50=5√2  см.

ВК=КС=5√2 см.

Рассмотрим ΔАВК - прямоугольный;  ∠ABK=90-60=30°

по теореме синусов sinA/BK=sin ABK/AK

AK=5√2*0,5:(√3/2)=(5√2)/√3=(5√6)/3 cм