Предмет: Математика,
автор: vladdzadziev
lim x стремится к 2 (ln(x^2-1)-ln(x+1))/((x-1)^(1/3)-1) вычислить предел
Приложения:
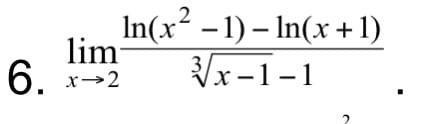
pushpull:
сложная запись предела. можно фото?
прикрепил
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
здесь надо применить правило Лопиталя
не, всё равно хрень
ну, не знаю я....
Я щас прикреплю ещё фото, как преподаватель ответил мне
Она написала, что нужно сделать, но у меня не получается все равно
я не могу отправить фото
я видела это фото в другом звдвнии .... пойду поищу, гляну... это там, где-таки домножать надо?
понятия не имею, мозги перестали работать, долго сижу с этим номером
домножить-то я домножила и получила (3ln(x-1))/(x-2) а дальше убей не понимаю, как у нее в конце концов пропал логарифм....
всё. я тупая. я решила. там надо домножить, получить в знаменателе х-2. в чмслителе разность логарифмов как логарифм частного и получится ln (x-1) а по второму замечательному пределу ln(x-1) ≈ x-2 и все. получается в ответе 3
где расписать?
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: fedorkostromin
Предмет: Математика,
автор: светлана53
Предмет: Математика,
автор: АйданаЖуматаева1
Предмет: Геометрия,
автор: Esik7