Предмет: Алгебра,
автор: narutolaa1
Найти производную, все показано на скриншоте
Приложения:
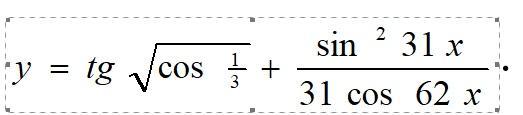
Ответы
Автор ответа:
2
Ответ:
первое слагаемое - числовые значение, так что производная 0.
Похожие вопросы
Предмет: Математика,
автор: krakasiabra
Предмет: Українська мова,
автор: mastertepla
Предмет: Математика,
автор: levhenko9
Предмет: Алгебра,
автор: rufyogesti
Предмет: Математика,
автор: TanyaTag