Предмет: Геометрия,
автор: zloymixa2006
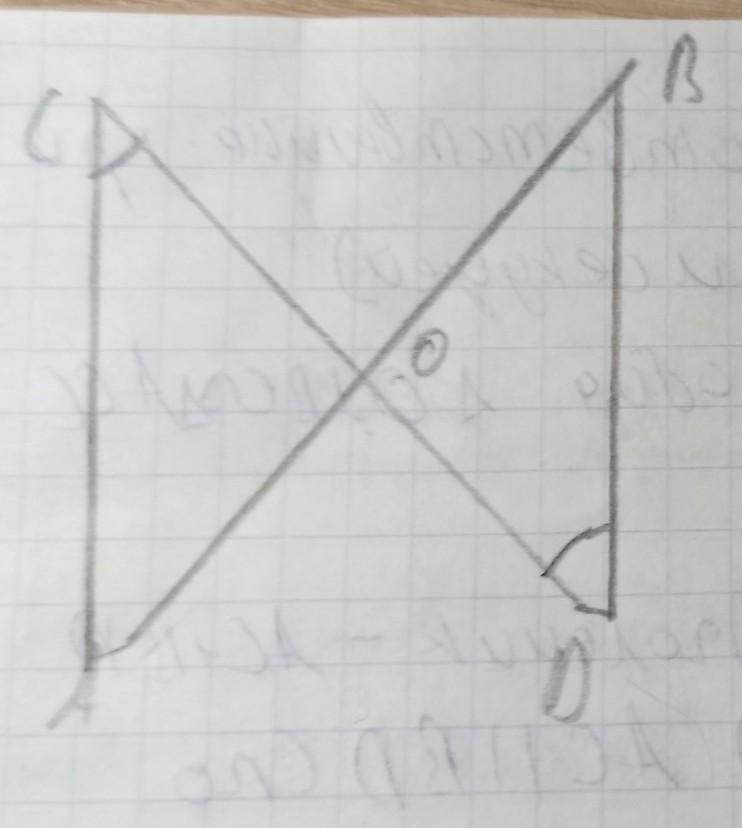
прямые CD и AB пересекаются в точке O, Известно что в треугольниках AOC и BOD угл ACO= углу BDO. AC=10,AO=12,BD=20,OD=16.найти OC и BD
Приложения:
Ответы
Автор ответа:
20
Ответ:
OC = 8
OD = 24
Объяснение:
Дано:
CD∩AB = O
∠ACO = ∠BDO
AC = 10, AO = 12, BD = 20, OD = 16.
Найти:
ОС, ОВ.
Решение:
∠ACO = ∠BDO по условию,
∠АОС = ∠BOD как вертикальные, значит
ΔAOC ~ ΔBOD по двум углам.
OB = 24
OC = 8
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: trufanova85
Предмет: Математика,
автор: vladik192
Предмет: Алгебра,
автор: Discorod
Предмет: Математика,
автор: 3Аня11111111111171
Предмет: Математика,
автор: Аноним