Предмет: Математика,
автор: roaprapr94
100 БАЛЛОВ ЗА ПРИМЕР
Приложения:
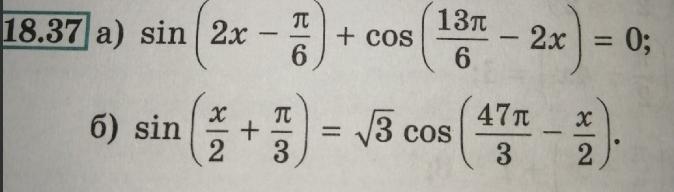
Ответы
Автор ответа:
1
Ответ:
a)
воспользуемся формулой приведения:
сложим синусы по формуле:
n принадлежит Z.
б)
косинусы сокращаются
n принадлежит Z
Похожие вопросы
Предмет: Қазақ тiлi,
автор: djangir560
Предмет: Математика,
автор: ILYA013
Предмет: Алгебра,
автор: vyrodovalara
Предмет: Математика,
автор: lelik551
Предмет: История,
автор: qwerty665
https://znanija.com/task/41902565