Предмет: Геометрия,
автор: garejsinaaziza
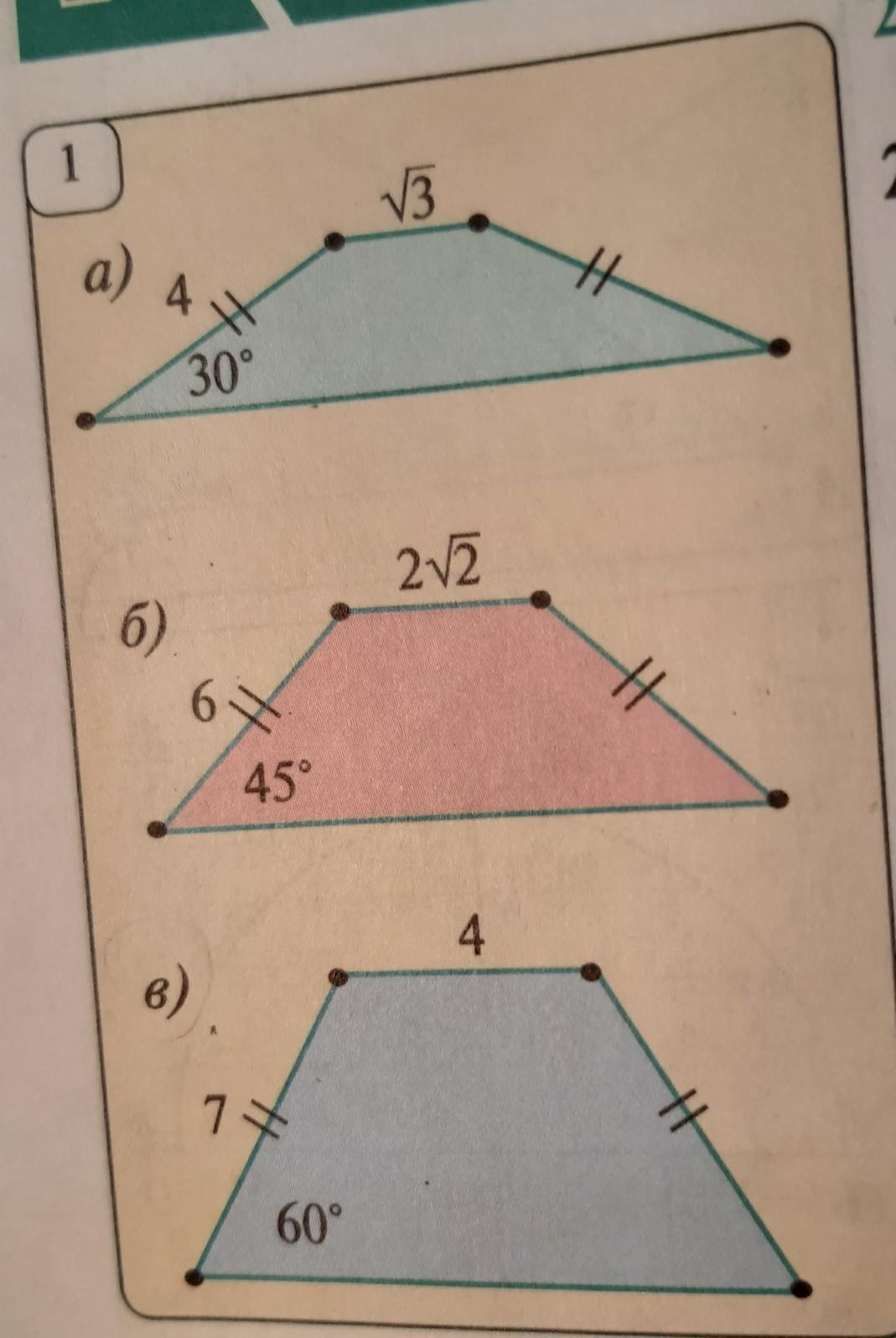
26.4. Используя данные рис.1, найдите площадь
рабнобедренной трапеции.
Приложения:
Ответы
Автор ответа:
64
Ответ:
Объяснение:
1)
Проведём две высоты ВК и CL
sin30°=BK/AB
BK=AB*sin30°=4*1/2=2
cos30°=AK/AB
AK=AB*cos30°=4*√3/2=2√3
АК=LD
BC=KL
AD=2*AK+KL=2*2√3+√3=5√3
S(ABCD)=BK(BC+AD)/2=2(√3+5√3)/2=6√3
Ответ: площадь трапеции равна 6√3.
2)
∆LMO- прямоугольный, равнобедренный треугольник LO=MO
LO=LM/√2=6/√2=3√2/√2=3√2.
OB=MN
LK=2*LO+OB=2*3√2+2√2=8√2.
S(LMNK)=MO(MN+LK)/2=3√2(2√2+8√2)/2=
=3√2*10√2/2=15*2=30
Ответ: площадь трапеции равна 30
3)
sin60°=BK/AB
BK=AB*sin60°=7*√3/2=3,5√3
cos60°=AK/AB
AK=AB*cos60°=7*1/2=3,5
AD=2*AK+BC=2*3,5+4=11
S(ABCD)=BK(BC+AD)/2=3,5√3(4+11)/2=
=3,5√3*15/2=26,25√3
Ответ: площадь трапеции равна 26,25√3
Приложения:

20mabel07:
спасибо
Похожие вопросы
Предмет: Другие предметы,
автор: nazerkenurkaii
Предмет: Русский язык,
автор: 25zx7c
Предмет: Русский язык,
автор: tatyanakalenko
Предмет: Физика,
автор: atambieva2003
Предмет: Химия,
автор: Saharo4ek01