Предмет: Математика,
автор: ilyaparamonov
Найти площадь фигуры ограниченной линиями (через интегралы)
Приложения:
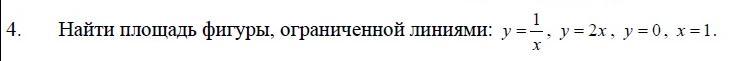
Ответы
Автор ответа:
0
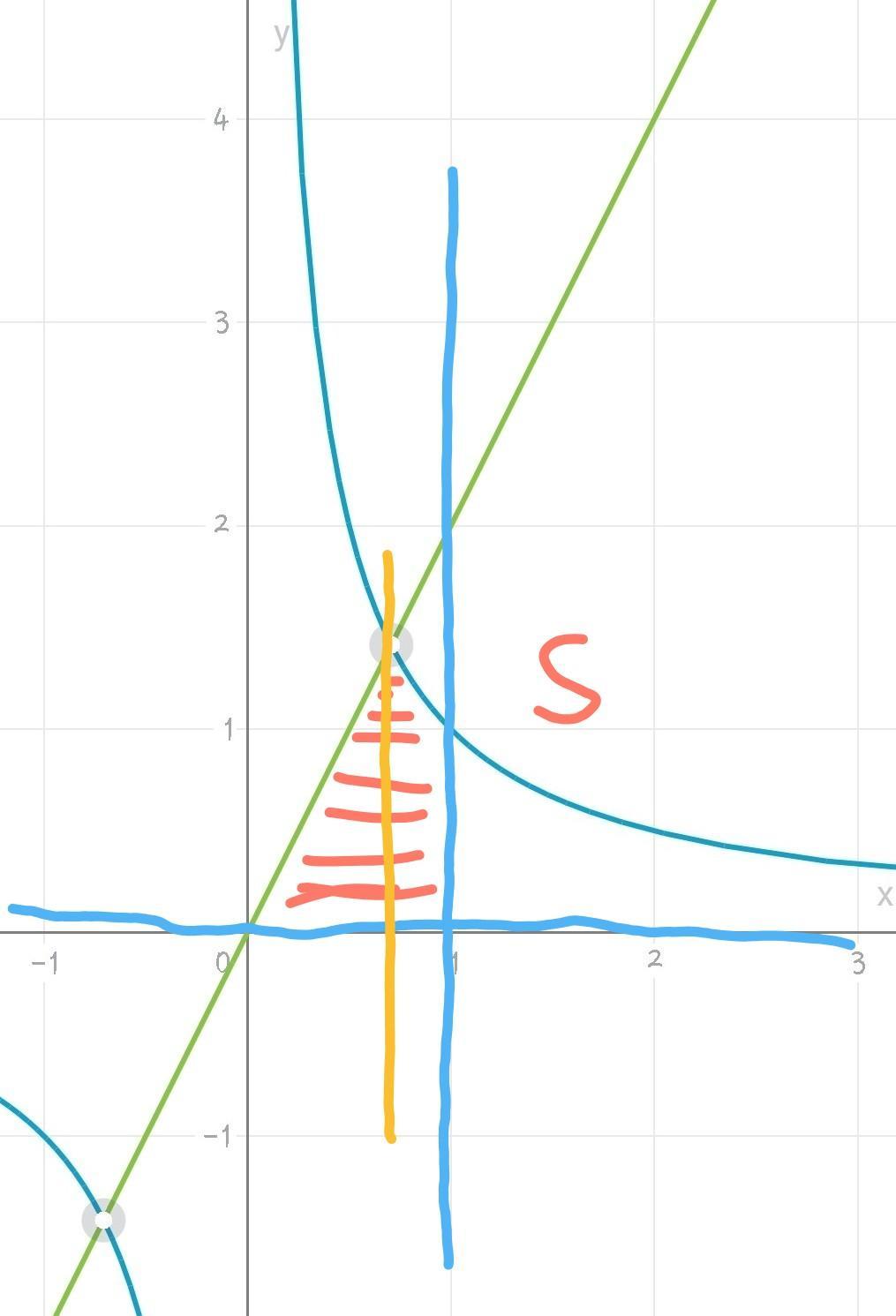
разделим на 2 фигуры и найдем 2 площади (разделила жёлтой линией).
Найдем точку пересечения двух функций:
нам подходит та, что > 0
S1 ищем от 0 до 1/(корень из 2), S2 от 1/(корень из 2) до 1.
если примерно посчитать, то
Приложения:
Похожие вопросы
Предмет: Математика,
автор: boloyang
Предмет: Математика,
автор: Arinaslaboda1
Предмет: Химия,
автор: lyuba010
Предмет: Литература,
автор: йыц