Предмет: Алгебра,
автор: Mixtit
Найти общее решение системы дифференциальных уравнений
Приложения:
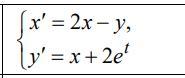
Ответы
Автор ответа:
2
Ответ:
подставляем (2) в (3)
это НЛДУ.
1)
2)
х с неопределенными коэффициентми:
подставляем в НЛДУ:
получаем общее решение х:
в итоге:
найдем у(t). Для этого найдем производную x(t)
подставляем (1) и (3) в (2):
Ответ:
Похожие вопросы
Предмет: Литература,
автор: Иля18
Предмет: Обществознание,
автор: annasliva
Предмет: Английский язык,
автор: apple55555
Предмет: Математика,
автор: romches222