Предмет: Математика,
автор: Ekaterina9888
Дана функция двух переменных . Проверить, выполняется ли тождество. СРОЧНО!
Приложения:
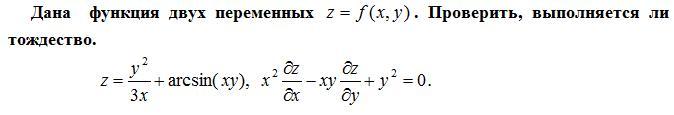
Ответы
Автор ответа:
1
Ответ:
подставляем в равенство:
равенство выполняется.
Mixtit:
Привет, прошу помоги с моими задачами по алгебре
Похожие вопросы
Предмет: Другие предметы,
автор: Demo20041
Предмет: Русский язык,
автор: evgen1106
Предмет: История,
автор: SinNasty
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: BROGGZI