Предмет: Математика,
автор: Аноним
Знайдіть похідні наступних функцій:
Приложения:
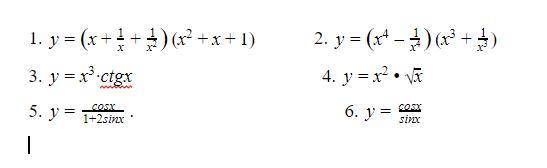
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
Похожие вопросы
Предмет: Литература,
автор: sobirovafarzon
Предмет: Русский язык,
автор: tema68
Предмет: Химия,
автор: Ella992901
Предмет: Математика,
автор: Novorussia2017