Предмет: Математика,
автор: 7thEXE
Помогите плиз, срочно!
Приложения:
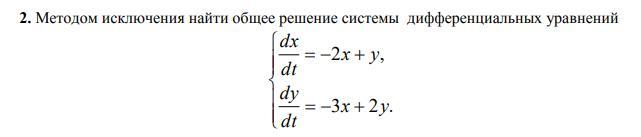
Ответы
Автор ответа:
2
Ответ:
(1) и (2) подставляем в (3)
получили:
(1) и (2) подставляем в (3)
Ответ:
Похожие вопросы
Предмет: Математика,
автор: yaskevich1998
Предмет: Математика,
автор: danilova19711
Предмет: История,
автор: evelinka1206
Предмет: Математика,
автор: 1234567891180
Предмет: Физика,
автор: Ṗṙĭṇṡḙṡṡkᾀ