У правільній шестікутній прізмі площа найбільшого діагонального перерізу 4 м, а відстань между двома протилежних бічнімі гранями 2 м. Знайте об'єм призми.
Ответы
Дано:
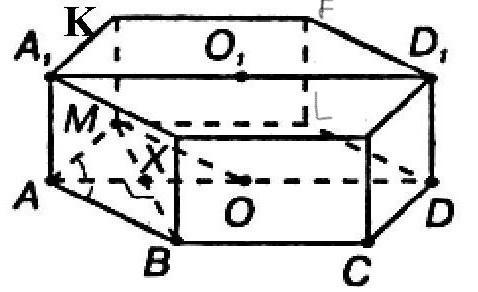
ABCDLMA₁B₁C₁D₁FK - правильная шестиугольная призма
AA₁D₁D - прямоугольник
S(AA₁D₁D) = 4 м²
MB = 2 м
-----------------------------------------------------------------------------------------
Найти:
V - ?
Решение:
Наибольшее диагональное сечение — это AA₁D₁D. Тогда AD — диаметр окружности, описанной около правильного шестиугольника. Так что AD=2R и АВ=АМ=R. ∠MAB найдем по формуле:
∠MAB = 180°×(n-2)/n = 180°×(6-2)/6 = 180°×4/6 = 30°×4 = 120°
Тогда: ∠MAX = 1/2 × ∠MAB = 1/2 × 120° = 60° ⇒ MX = 1/2 × MB = 1/2 × 2 м = 1 м
Далее, мы находим сторону AX из прямоугольного ΔАМХ:
AM = MX/sin∠MAX = 1 м/sin 60° = 1 м/√3/2 = 1 м × 2/√3 = 2/√3 м × √3/√3 = 2√3/3 м ⇒ R = AM = 2√3/3 м
Значит что сторона AD будет равен:
AD = 2R = 2 × 2√3/3 м = 4√3/3 м
Теперь находим высоту AA₁ с помощью формулы прямоугольника AA₁D₁D:
S(AA₁D₁D) = AA₁ × AD - площадь прямоугольника
4м² = AA₁ × 4√3/3 м ⇒ AA₁ = 4м²/4√3/3 м = 4×3/4√3 м = 12/4√3 м × √3/√3 = 12√3/4×(√3)² м = 12√3/4×3 м = 12√3/12 м = √3 м
Далее, мы находим площадь основания правильной шестиугольной призмы, мы знаем площадь основания равна площади шести равносторонних, то есть:
Sосн = 6S(ΔAMO) = 6×1/2×MO×AO×sin 60° = 6×1/2×(2√3/3 м)² × √3/2 = 3 × 12/9 м² × √3/2 = 3 × 4/3 м² × √3/2 = 4 м² × √3/2 = 2√3 м²
И теперь находим объем правильной шестиугольной призмы:
V = Sосн × h = Sосн × AA₁ = 2√3 м² × √3 м = 2×(√3)² м³ = 2×3 м³ = 6 м³
Ответ: V = 6 м³
P.S. Рисунок показан внизу↓