Предмет: Математика,
автор: HappyWorld
Найти первую и вторую производные
Приложения:
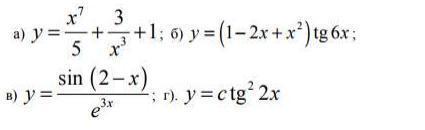
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
г)
Похожие вопросы
Предмет: История,
автор: еленакласс
Предмет: Русский язык,
автор: 051102таня
Предмет: Литература,
автор: 52anya28
Предмет: Математика,
автор: dianagnunyan