помогите решить это пожалуйста
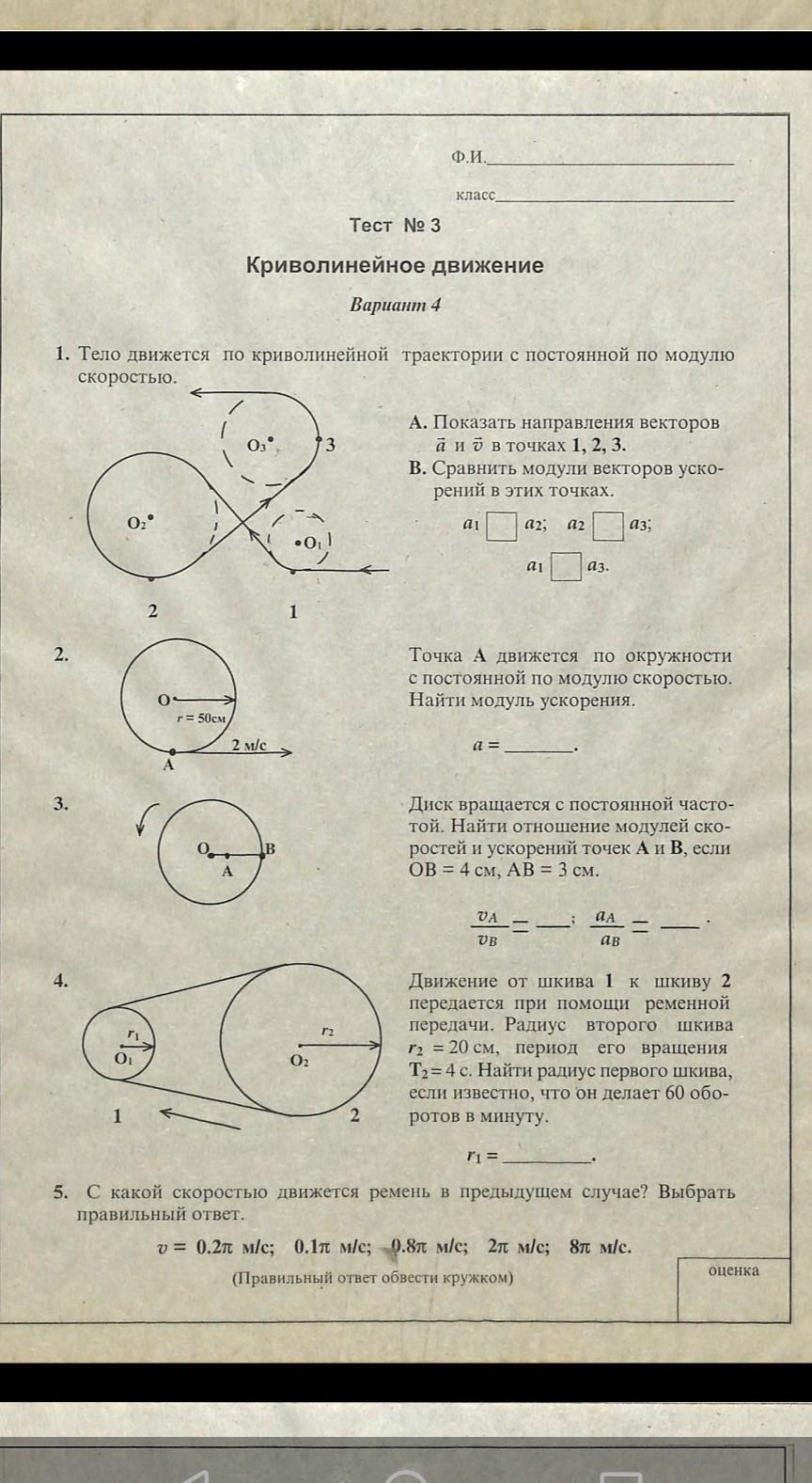
Ответы
Ответ:
[Скриншот во вложении]
Объяснение:
1. Вектор скорости при криволинейном движении всегда направлен по касательной к кривой траектории движения. Модуль ускорения при таком движении состоит из тангенциального () и нормального (
) ускорений:
Тангенциальное ускорение выражает изменение модуля скорости, его вектор сонаправлен с вектором скорости - по касательной к траектории движения. Нормальное ускорение выражает изменение скорости по направлению, поэтому оно всегда направлено в центр окружности, соответствующей рассматриваемому участку кривой траектории движения.
В данном примере движение равномерное, поэтому тангенциальное ускорение отсутствует. Следовательно, значения сравниваемых модулей ускорения обозначенных точек выражаются так:
2. Модуль скорости снова постоянный, поэтому тангенциальное ускорение отсутствует, и модуль ускорения равен:
3. Частота вращения постоянная → модули скорости точек постоянны → тангенциальное ускорение отсутствует.
Находим радиус OA: OA = OB - OA = 4 - 3 = 1 см
Модуль скорости вращения определяется угловой скоростью вращения и радиусом:
Поэтому соотношение модулей скорости точек А и В c учетом соотношения их модулей скорости следующее:
Соотношение модулей ускорений (без тангенциальных ускорений) следующее:
4. Так как шкивы соединены ременной передачей, их модули скорости равны. Поэтому по ней будем искать радиус первого шкива.
Скорость вращения шкива определяется по периоду его вращения и длине его окружности:
Первый шкив совершает 60 оборотов в минуту = 1 оборот в секунду, поэтому его период оборота равен 1 сек. Отсюда получаем радиус шкива:
5. В предыдущей задаче шкив двигался со скоростью 10π см/с, то есть 0.1π м/с
