Question

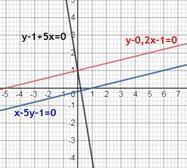
L : x-5y-1=0
M(0;1)
......................

Answer 1

Ответ:

Пошаговое объяснение:

$L: x-5y-1=0\\M(0;1)$

а) расстояние от точки до прямой (уравнение прямой задано в общм виде Ах + Ву + +С = 0)

$p=\frac{IA*M_x+B*M_y+CI}{\sqrt{A^2+B^2} } =\frac{I1*0+(-5)*1+(-1)I}{\sqrt{1^2+(-5)^2} } =\frac{6}{\sqrt{26} } =\frac{3\sqrt{26} }{13}$

б) вектор нормали прямой L   $n_L=(1;-5)$   он же и направлющий для нужной нам прямой $s_{L'}=(1;-5)$

уравнение прямой через точку по направляющему вектору

$\frac{x-0}{1} =\frac{y-1}{-5} ;$ это и есть уравнение прямой L' в общем виде 5х +у -1 =0

в)

ну, самый легкий путь.

представим наше уравнение L в виде уравнения с угловым коэффициентом

у = 0,2х -0,2   и тогда

уравнение L'' параллельно L находим по формуле:

y - y₀ = k(x - x₀)

подставим  $x_0=x_M$ (проходіт через точкуМ)

k = 0.2, тот же коэффициент, что и у L, т.к. они параллельны

$y_0=y_M=1$

получим уравнение прямой L", параллельнойй прямой L в виде уравнения с угловым коэффициентом

y-1 = 0.2(x-0)

или

y = 0.2x + 1

в общем виде уравнение  L"

 y - 0.2x -1 =0