Предмет: Алгебра,
автор: romapetrosyan2019
Помогите срочно надо
Приложения:
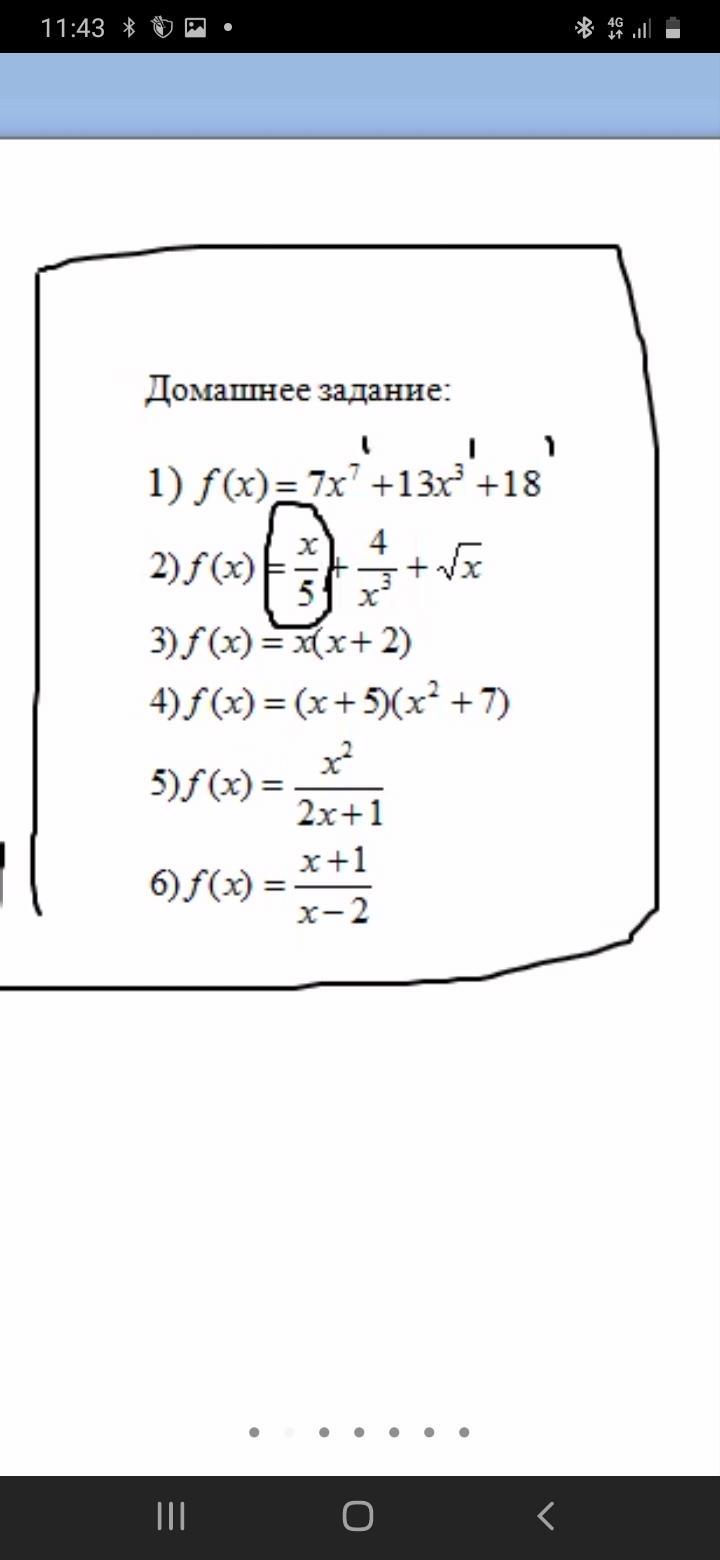
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
Похожие вопросы
Предмет: Математика,
автор: denis2002i
Предмет: Алгебра,
автор: fffffffffff1
Предмет: Математика,
автор: капарка
Предмет: Математика,
автор: Armenianrambo1000