Предмет: Геометрия,
автор: znatok4630
Площади параллелограмма и ромба. Урок 1
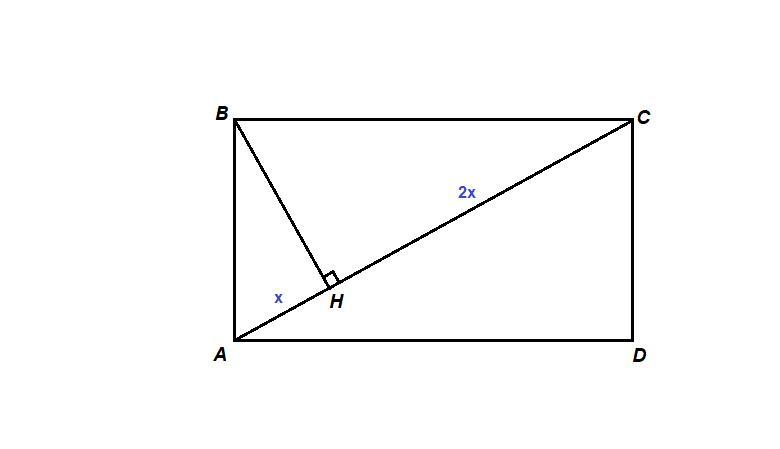
Высота прямоугольника, опущенная на диагональ с длиной 9 см, делит эту диагональ в отношении 1 : 2. Найди площадь прямоугольника.
Высота, опущенная на диагональ:
Площадь прямоугольника:
пожалуйста помогите решить
Приложения:

Ответы
Автор ответа:
1
Ответ:
Высота, опущенная на диагональ: 3√2 см
Площадь прямоугольника: 27√2 см²
Объяснение:
АС = 9 см
ВН⊥АС
АН : НС = 1 : 2
Пусть АН = х, тогда НС = 2х.
АС = АН + НС
x + 2x = 9
3x = 9
x = 3
АН = 3 см
НС = 3 · 2 = 6 см
- В прямоугольном треугольнике высота, проведенная к гипотенузе равна среднему геометрическому отрезков, на которые разбивается гипотенуза.
ΔАВС: ∠АВС = 90°,
ВН² = АН · НС = 3 · 6 = 18
ВН = √18 = 3√2 см
см²
Диагональ разбивает прямоугольник на два равных треугольника, значит площадь прямоугольника в два раза больше площади треугольника АВС.
см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: faiza2002
Предмет: Физика,
автор: Mozartienne
Предмет: Другие предметы,
автор: natali039
Предмет: Математика,
автор: zhannaray
Предмет: История,
автор: esedov19791