Question

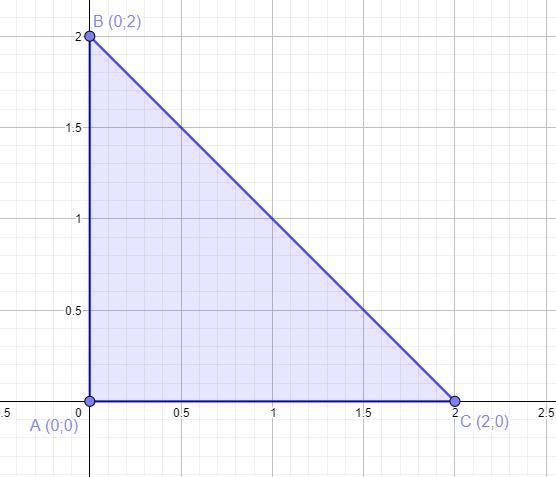
Определите вид треугольника ABC, если его вершины имеют координаты A(0; 0), B(0; 2) и C(2; 0)​

Answer 1

Ответ:

Прямоугольный

Объяснение:

По формуле расстояния между двумя точками на координатной плоскости:

$AB = \sqrt{(x_{B} - x_{A})^{2} + (y_{B} - y_{A})^{2}} = \sqrt{(0 - 0)^{2} + (2 - 0)^{2}} = \sqrt{2^{2}} = 2$

$CB = \sqrt{(x_{B} - x_{C})^{2} + (y_{B} - y_{C})^{2}} = \sqrt{(0 - 2)^{2} + (2 - 0)^{2}} = \sqrt{2^{2} + 2^{2}} =$

$= \sqrt{4 + 4} = \sqrt{8}$

$AC = \sqrt{(x_{C} - x_{A})^{2} + (y_{C} - y_{A})^{2}} = \sqrt{(2 - 0)^{2} + (0 - 0)^{2}} = \sqrt{2^{2}} = 2$

По теореме косинусов для треугольника ΔABC:

$AB^{2} + AC^{2} - 2 \cdot AB \cdot AC \cdot \cos \angle BAC = BC^{2}$

$\cos \angle BAC = \dfrac{AB^{2} + AC^{2} - BC^{2}}{2 \cdot AB \cdot AC} = \dfrac{2^{2} + 2^{2} - (\sqrt{8} )^{2}}{2 \cdot 2 \cdot 2} = \dfrac{4 + 4- 8 }{8} = \dfrac{0}{8} = 0$.

$\cos \angle BAC = 0 \Longrightarrow \angle BAC = 90^{\circ}$. Так как угол ∠BAC = 90°, то треугольник ΔABC - прямоугольный.