Предмет: Математика,
автор: Pop2121
СРОЧНО!!ГЕОМЕТРИЯ
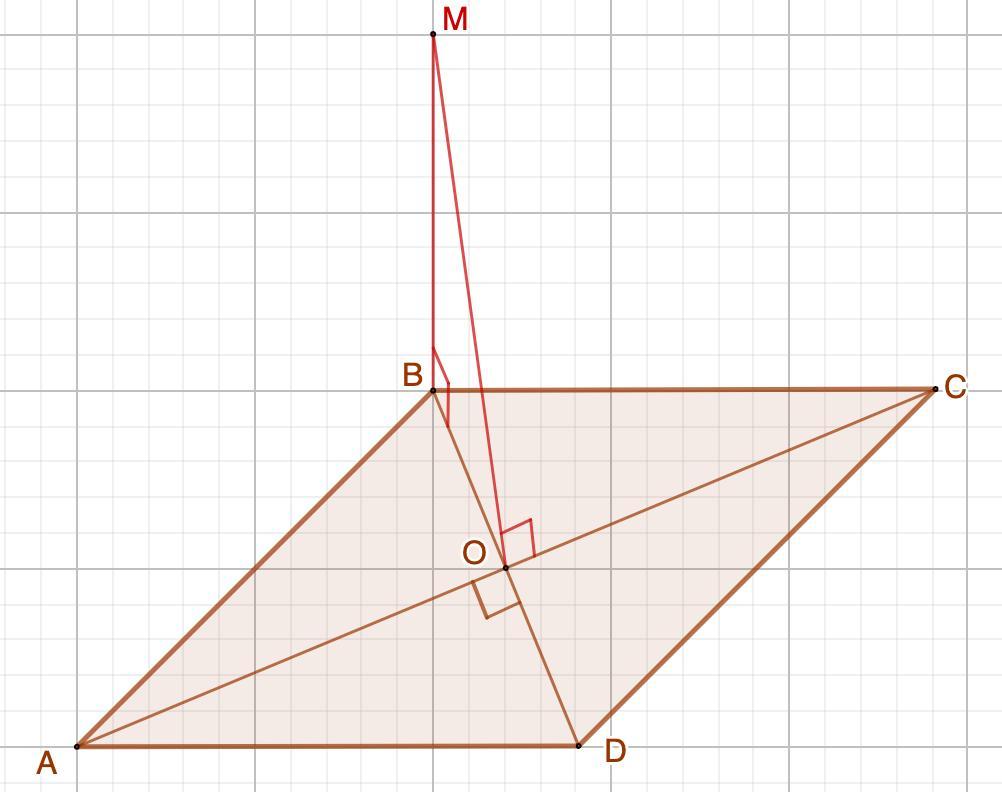
Через вершину B ромба ABCD проведена прямая BM, перпендикулярная плоскости ромба. Найдите расстояние от точки M до прямой AC, если MB=12 см, DC=16 см, AC=20 см.
Ответы
Автор ответа:
15
Ответ:
МО=10√3 см
Пошаговое объяснение:
Дано: ABCD - ромб
MB⊥ABCD
MB=12 см; DC=16 см; АС=20 см.
Найти: МО.
Решение:
Расстояние от точки до прямой - перпендикуляр опущенный из этой точки на данную прямую.
Диагонали ромба пересекаются под прямым углом.
⇒ Искомое расстояние - МО (теорема о трех перпендикулярах).
1. Рассмотрим ΔАВО - прямоугольный.
АВ=16 см (стороны ромба равны)
АО=ОС=20:2=10 (см) (диагонали точкой пересечения делятся пополам)
По теореме Пифагора:
2. Рассмотрим ΔВМО - прямоугольный.
По теореме Пифагора:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: aaa010282
Предмет: Математика,
автор: Marian200075
Предмет: Математика,
автор: arinina2003
Предмет: Математика,
автор: 87006071981
Предмет: Математика,
автор: Ирина5866