Предмет: Алгебра,
автор: plastik123
Система уравнений..............
Приложения:
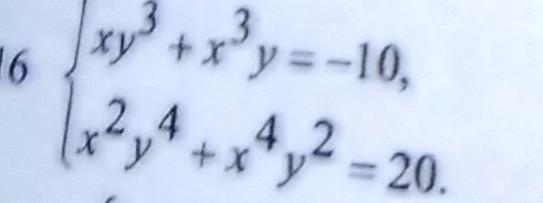
plastik123:
чел ты....
зачем меня учить системам 5 класса?
я их не знаю что-ли
чел
я не сделал
поэтому кинул сюда задание
мне нужно решение
а не ответ
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Rif150
Предмет: Литература,
автор: kalupas542
Предмет: Химия,
автор: leksik578
Предмет: Физика,
автор: ek862385
Предмет: Математика,
автор: МазурСаша