Предмет: Геометрия,
автор: coolman9152
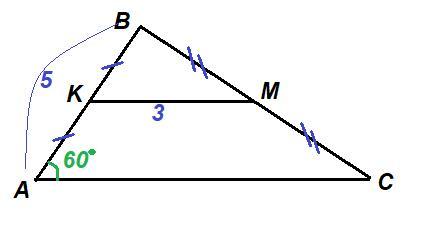
В треугольнике ABC AB = 5 см, ∠A = 60°, отрезок, соединяющий середины сторон AB и BC, равен 3 см. Найди периметр треугольника ABC.
Ответы
Автор ответа:
6
Дано: ΔABC, AB = 5 см, ∠А = 60°,
K∈AB, AK=KB, M∈BC, BM=MC, KM = 3 см.
Найти:
Решение:
Средняя линия треугольника - отрезок, соединяющий середины двух сторон, - равна половине третьей стороны:
KM = AC : 2 ⇒ AC = 2·KM = 2·3 = 6 см
По теореме косинусов:
Ответ: (11+√31) см
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: физика77
Предмет: Математика,
автор: Пётр10
Предмет: Математика,
автор: v98041
Предмет: История,
автор: лучший54