Предмет: Математика,
автор: aezzaxproven
Используя формулу логарифмического дифференцирования, найти производные следующих функций:
Приложения:
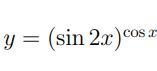
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Химия,
автор: ulyananesterovaa
Предмет: Физика,
автор: catsssss
Предмет: Математика,
автор: zamshasonya271
Предмет: Математика,
автор: stervo4ka2007