Предмет: Геометрия,
автор: maks220418
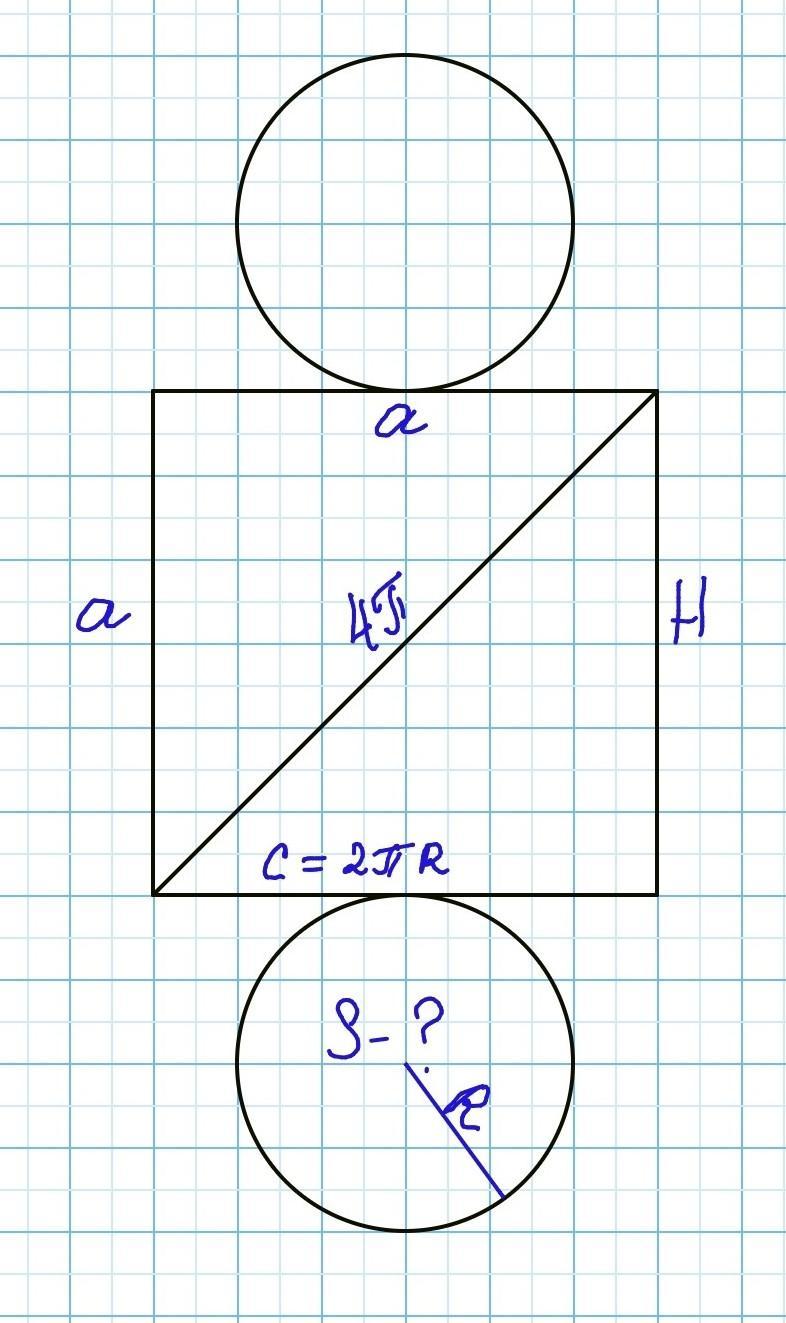
Квадрат, діагональ якого дорівнює 4π см, є розгорткою бічної поверхні
циліндра. Знайдіть площу основи цього циліндра.
Ответы
Автор ответа:
2
Ответ: 2π см²
Розгортка бічної поверхні циліндра - квадрат, одна сторона якого дорівнює висоті циліндра, а друга сторона - є довжиною кола основи циліндра: C=2πR, R -радіус кола основи.
Діагональ квадрата:
где а- сторонна квадрата.
=> Сторона квадрата:
Так як за умовою сторона квадрата дорівнює довжині кола (а=С), то:
Радіус основи R дорівнює √2 см.
Площа основи циліндра: S(кола)= πR²= π(√2)²=2π см²
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: sumka135
Предмет: Русский язык,
автор: lubovkorsh
Предмет: Математика,
автор: митя4
Предмет: Биология,
автор: wolkowartur807
Предмет: Математика,
автор: МаНдАрИнЧиК2018