Предмет: Математика,
автор: anastasiygal
Очень нужно решение одного из примеров(интегралы)
Приложения:
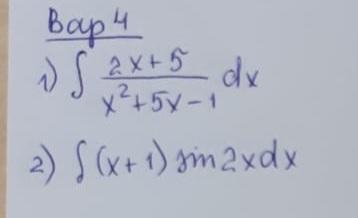
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1)
2)
Похожие вопросы
Предмет: Биология,
автор: sonya1348
Предмет: Алгебра,
автор: machete6211
Предмет: Математика,
автор: rubanton
Предмет: Математика,
автор: АнгеЛОчек112