Предмет: Геометрия,
автор: pisslina66
признаки и свойства. Урок 2
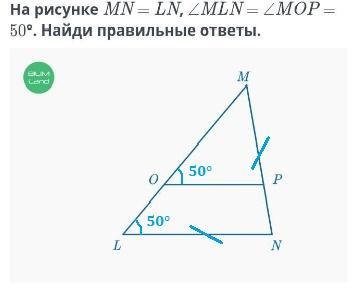
На рисунке MN = LN, MLN = 2 МОР
50°. Найди правильные ответы.
Приложения:
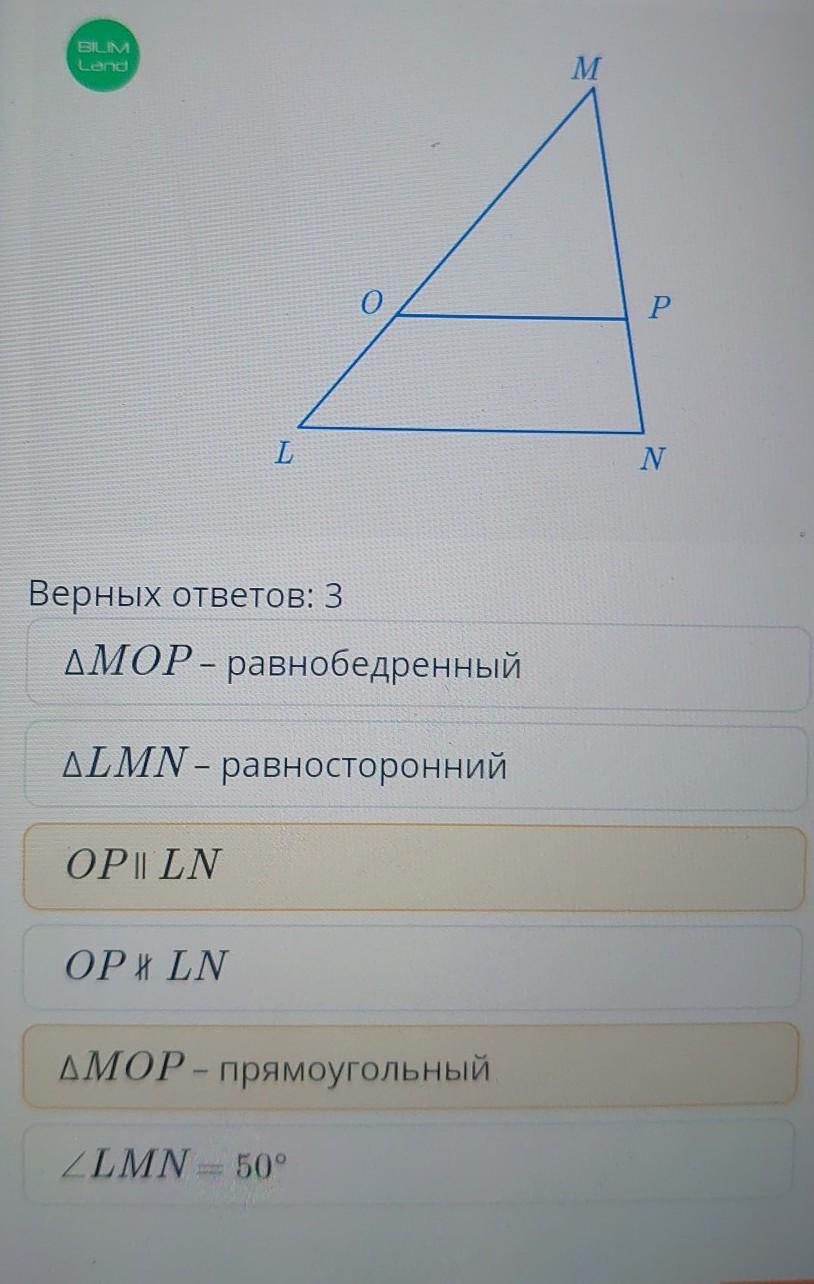
Ответы
Автор ответа:
1
Ответ:
1) ОР ║ LN
2) ∠LMN = 50°
3) ΔМОР - равнобедренный.
Объяснение:
1) ∠МОР и ∠MLN - соответственные углы, образованные при при пересечении двух прямых ОР и LN секущей ML.
Если соответственные углы равны, то прямые параллельны.
Следовательно: ОР ║ LN
2) Так как MN = LN, MN и LN - боковые стороны ΔMNL, то ΔMNL - равнобедренный.
- Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им - основание.
В равнобедренном треугольнике углы при основании равны.
∠LMN =∠MLN = 50°
3) Так как ∠LMN =∠МОР, то треугольник МОР - равнобедренный.
- Если углы при основании равны, то треугольник равнобедренный.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: belekmonge3
Предмет: Другие предметы,
автор: oktixomirova
Предмет: Математика,
автор: kishinskaya74илья
Предмет: Информатика,
автор: 20vanya02
Предмет: Математика,
автор: Djessika24