Предмет: Геометрия,
автор: radriges1uno
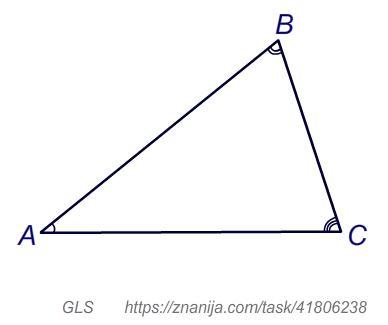
Дан треугольник ABC. Выполни соответствие
Приложения:

Ответы
Автор ответа:
1
Ответ:
Соответствие: 1 - 2; 2 - 1; 3 - 3.
Объяснение:
- По теореме косинусов:
- квадрат стороны треугольника равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними.
Выразим косинус каждого угла в соответствии с теоремой косинусов.
1)
Соответствие 1 - 2.
2)
Соответствие 2 - 1.
3)
Соответствие 3 - 3.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: tatsergei
Предмет: Математика,
автор: naumenkotamila57815
Предмет: Биология,
автор: Дашка1357
Предмет: Математика,
автор: Doshin1
Предмет: Физика,
автор: шаосдигя