Question

у трикутнику АВС точки М іР середини сторін АВ і ВС відповідно. знайдіть координати точкиС якщо А(0;2), М(3;5) Р (7;4). Розв'яжіть задачу 2 способами ​

Answer 1

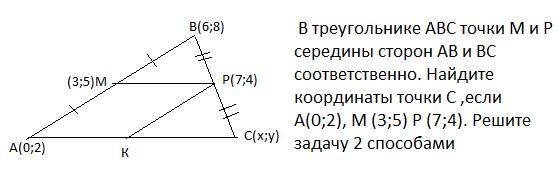
В треугольнике АВС точки М и Р середины сторон АВ и ВС соответственно. Найдите координаты точки С ,если А(0;2), М (3;5) Р (7;4). Решите задачу 2 способами

Объяснение:

1 способ.

Пусть РК║АВ , тогда К -середина АС , по т. Фалеса. АМРК-параллелограмм по определению.Вектор МА(0-3;2-5) или МА(-3 ;-3) *****Пояснение-Точка А получена параллельным переносом точки М на вектор МА . И точка К может быть получена точно таким же параллельным переносом точки Р в точку К параллельным переносом на вектор МА . *****

х(К)=х(Р)+х(МА) ⇒ х(К)=7+(-3)=4,у(К)=у(Р)+у(МА) ⇒ х(К)=4+(-3)=1 . Значит точка К(4; 1).

Для отрезка АС точка К-середина. По формулам середины отрезка ищем координаты точки С :     $x(K)=\frac{x(A)+x(C)}{2 } ,$   х(С)=2*х(К)-х(А) или х(С)=8-0=8 . Аналогично у(С)=2-2=0 . Поэтому С(8;0).

2 способ.

Для отрезка ВС точка Р-середина. По формулам середины отрезка ищем координаты точки Р :  $x(P)=\frac{x(B)+x(C)}{2 } ,$   х(С)=2*х(Р)-х(В) или х(С)=14-6=8 . Аналогично у(С)=8-8=0 . Поэтому С(8;0)