Помогите пожалуйста
Ответы
Ответ:
(см. объяснение)
Объяснение:
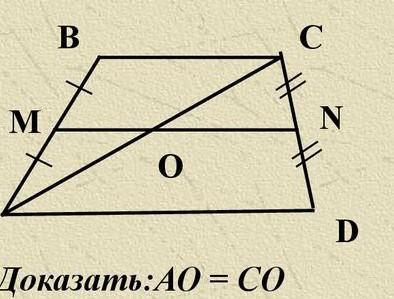
Т.к. M и N середины сторон AB и CD, то MN - средняя линия трапеции ABCD по определению. Тогда MN||AD. Рассмотрим треугольник ACD. В нем CN=ND (N - середина CD) и ON||AD. Значит ON средняя линия треугольника ACD по признаку средней линии. Тогда O - середина AC, т.е. AO=CO.
Доказано!
Приведу пример другого доказательства:
(все дополнительные построения приведены в прикрепленном файле)
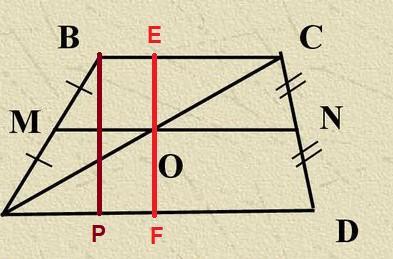
Проведем через точку O прямую, перпендикулярную AD и BC. Пусть эта прямая пересекает BC в точке E, а AD в точке F. Получим два треугольника: COE и AOF. Понятно, что ∠CEO=∠AFO=90° (по построению), а ∠AOF=∠COE (вертикальные). Покажем, что EO=FO. Проведем прямую, параллельную EF и проходящую через точку B. Пусть она пересекает отрезок AD в точке P. Получили BP=EF. Из подобия треугольников в свою очередь получим, что высота трапеции делится ее средней линией пополам. Но тогда ΔCOE=ΔAOF. Значит AO=CO.
Доказано!