Предмет: Алгебра,
автор: LAGEP
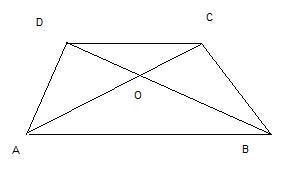
Диагонали трапеции ABCD c основанием AB и CD пересекаются в точке O. Найдите AO, если AB=9,6 дм, DC=24 см, AC=15 см. Приз помогите
LAGEP:
Хэлп
Ответы
Автор ответа:
1
Ответ:
1. Треугольники DOC и АОВ подобны по первому признаку подобия треугольников: два угла одного треугольника соответственно равны двум углам другого. В нашем случае углы DOC и АОВ равны как вертикальные углы, а углы DCA и САВ равны как накрест лежащие углы при пересечении параллельных прямых DC и АВ секущей АС.
2. Выразим ОС как 15-АО
3. Поскольку треугольники подобны, можно записать:
АО / ОС = АВ / DC,
АО = ОС*АВ / DC
AO = (15-AO)*AB / DC
AO = (15-AO)*96 / 24
24AO = (15-AO)*96
24AO = 1440 - 96AO
120AO = 1440
AO = 12 см
Объяснение:
Приложения:
А это правильно?
По крайней мере, для многих да.
Ну ладно
Пасиба!
Не за что
А у тебя дс есть?
Автор ответа:
1
Ответ:
на фото..............
Приложения:

Похожие вопросы
Предмет: Химия,
автор: gladilina28
Предмет: Математика,
автор: kbarg
Предмет: Английский язык,
автор: a5n
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: никита3605