Question

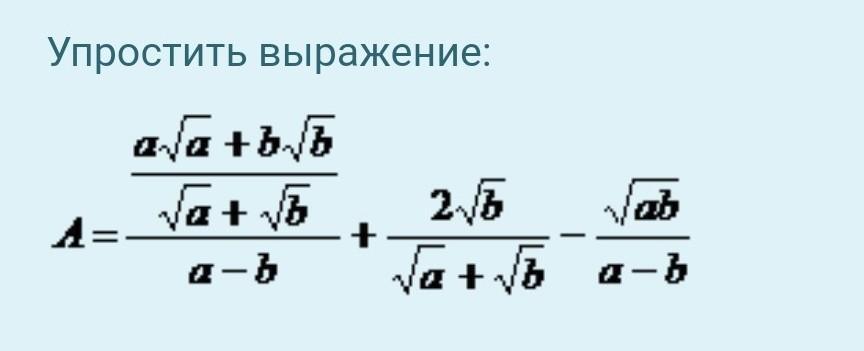
алгебра упростите выражение ​

Answer 1

Ответ:

$\frac{ \frac{a\sqrt{a} + b \sqrt{b} }{ \sqrt{a} + \sqrt{b} } }{a- b} + \frac{2 \sqrt{b} }{ \sqrt{a} + \sqrt{b} } - \frac{ \sqrt{ab} }{a - b} = \\ = \frac{a \sqrt{a} + b \sqrt{b} }{(a - b)( \sqrt{a} + \sqrt{b} )} + \frac{2 \sqrt{b} }{ \sqrt{a} + \sqrt{b} } - \frac{ \sqrt{ab} }{a - b} = \\ = \frac{a\sqrt{a} + b \sqrt{b} + 2 \sqrt{b} (a- b) - \sqrt{ab}( \sqrt{a} + \sqrt{b} )}{(a - b)( \sqrt{a} + \sqrt{b}) } = \\ = \frac{a \sqrt{a} + b\sqrt{b} + 2a \sqrt{b} - 2b \sqrt{b} - a \sqrt{b} - b \sqrt{a} }{(a - b)( \sqrt{a} + \sqrt{b}) } = \\ = \frac{a\sqrt{a} - b\sqrt{b} + a \sqrt{b} - b\sqrt{a} }{(a- b)( \sqrt{a} + \sqrt{b}) } = \\ = \frac{ \sqrt{a} (a - b) + \sqrt{b}(a- b) }{(a- b)( \sqrt{a} + \sqrt{b} )} = \frac{(a- b)( \sqrt{a} + \sqrt{b} )}{(a - b)( \sqrt{a} + \sqrt{b} )} = 1$

Answer 2

Ответ:

a-b

Объяснение:Приводим к общему знаменателю, учитывая что (a-b) по формуле разности квадратов равно $x-y=(\sqrt{x} -\sqrt{y} )*(\sqrt{x} +\sqrt{y} )$получим A=$((a\sqrt{a} +b\sqrt{b} )/(\sqrt{a} +\sqrt{b} )+(2\sqrt{b}*(\sqrt{a} -\sqrt{b} )-(\sqrt{ab} ))/(a-b)$Проведя перемножение и группировку подобных членов получим:

A=$(a\sqrt{a} +b\sqrt{b} +2a\sqrt{b}-2b\sqrt{b} -a\sqrt{b} -b\sqrt{a} )/(a-b)$

Далее группируя подобные получим  A= a-b