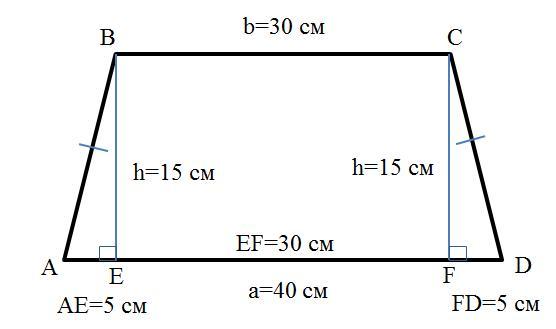
Основания равнобедренной трапеции 40 см и 30 см, а высота 15 см. Найдите площадь трапеции,
разделив ее на части.
Ответы
Ответ:
525 см²
Объяснение:
Проведём высоты BE и CF (см. рисунок). Тогда трапеция делится на 3 части:
BEFC – прямоугольник: длина BC=EF=30 см и ширина h=BE=CF=15 см;
ΔABE – прямоугольный с катетами: h=BE=15 см и AE;
ΔDCF – прямоугольный с катетами: h=CF=15 см и DF.
Так как трапеция равнобедренный, то по признаку равенства прямоугольных треугольников по катету и гипотенузе, треугольники ΔABE и ΔDCF равны, следовательно, AE=DF. Поэтому
AE=DF=(AD–BC):2=(40–30):2=10:2=5 см.
Теперь площадь трапеции определим как сумма площадей частей:
S(ABCD)=S(ΔABE)+S(BEFC)+S(ΔDCF)=2•S(ΔABE)+S(BEFC).
Площадь прямоугольника определяется через длину и ширину по формуле
S = длина • ширина.
Отсюда
S(BEFC)= BC•BE=30•15=450 см².
Площадь прямоугольного треугольника определяется через катеты по формуле
S = катет1 • катет2/2.
Следовательно:
S(ΔABE)=S(ΔDCF)=BE•AE/2=15•5/2=75/2=37,5 см².
Тогда площадь трапеции равна
S(ABCD)=2•S(ΔABE)+S(BEFC)=2•37,5+450=75+450=525 см².