Предмет: Геометрия,
автор: marinagor2012
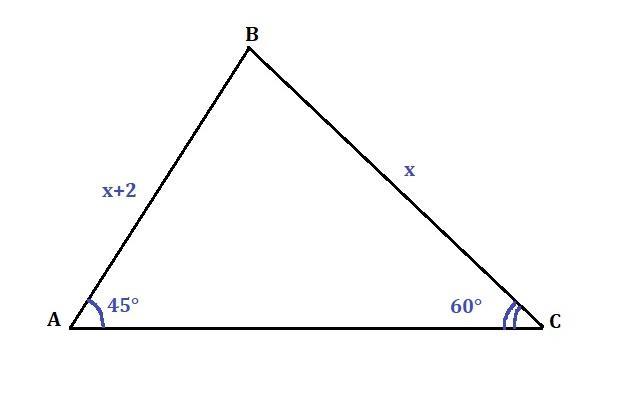
Дан треугольник ABC. Если AB – BC = 2 см, ∠A = 45° и ∠C = 60°, то найди длины сторон AB и BC.
Ответы
Автор ответа:
2
Ответ:
АВ = (2√6+6) см
ВС = (2√6+4) см
Объяснение:
Пусть ВС = х см, тогда АВ=ВС+2 = (х+2) см
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.
По теореме синусов:
Избавимся от иррациональности в знаменателе. Для этого числитель и знаменатель умножим на одно и тоже число: (√3+√2):
Сторона ВС = (2√6+4) см
АВ = 2√6+4 + 2 = (2√6+6) см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: bkru2000
Предмет: Биология,
автор: 2002крис2002
Предмет: Русский язык,
автор: Каро1
Предмет: Информатика,
автор: kanikovaalbina
Предмет: Математика,
автор: Karina12311111