Предмет: Математика,
автор: epishin0404
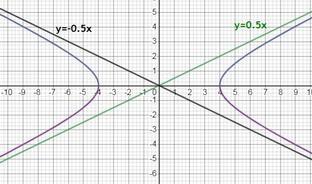
Построить график и определить асимптоты гиперболы x^2-4y^2=16
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
x²-4y²=16 ⇒
т.е. наша функция иммет такой вид
1)
уравнение ищем в виде y = kx + b
из определения асимптоты найдем k и b
определениe , откуда
итак, мы получили уравнение наклонной асимптоты
y = 0.5x
2)
совершенно аналогично мы получим
и получим другое уравнение асимптоты
y = -0.5x
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Rizhik8
Предмет: Математика,
автор: kolesnikovn
Предмет: Русский язык,
автор: manykyanishkha
Предмет: Математика,
автор: Winter124
Предмет: Алгебра,
автор: миха1234578