Предмет: Алгебра,
автор: evgisaev2013
Найди точки экстремума и значения функции в этих точках
y=x^3+2x^2/(x-1)^2
Ответы
Автор ответа:
0
Находим производную:

Находим стационарные точки(точки в которых производная равна нулю):

х=-1 - точка максимума.
х=4, x=0 - точки минимума

По вопросам в личку.
Находим стационарные точки(точки в которых производная равна нулю):
х=-1 - точка максимума.
х=4, x=0 - точки минимума
По вопросам в личку.
Приложения:
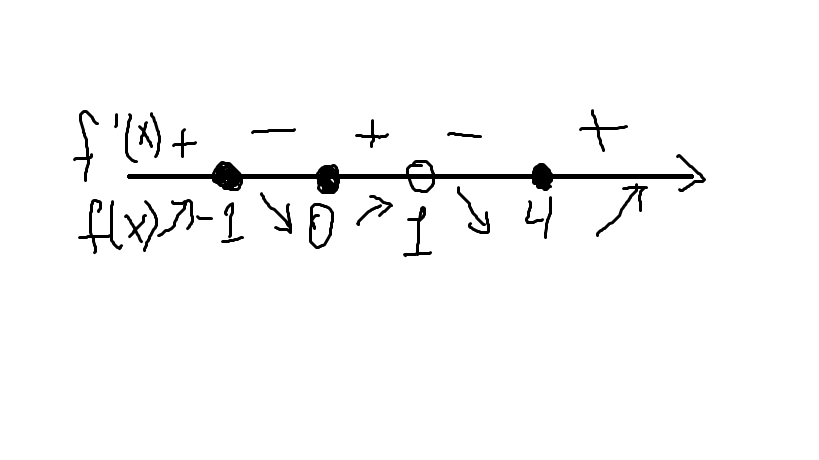
Похожие вопросы
Предмет: Английский язык,
автор: lipka8
Предмет: Математика,
автор: Roma000111
Предмет: Английский язык,
автор: gooruknig
Предмет: Геометрия,
автор: li0ness
Предмет: Химия,
автор: anastasiyadomar