Предмет: Математика,
автор: berill1997
Помогите найти производные функций
Приложения:
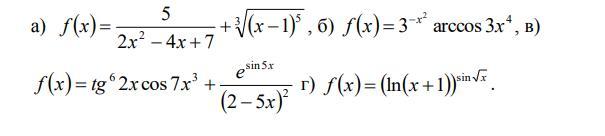
Ответы
Автор ответа:
0
Пошаговое объяснение:
а)
б)
в)
г)
формула:
KACAHAP:
мен помогите по математике пж
мне помогите по матемптике пжжжж
Похожие вопросы
Предмет: Русский язык,
автор: 1Cаша1
Предмет: Математика,
автор: Love2Eat
Предмет: География,
автор: angelosheknet
Предмет: Математика,
автор: alisamalandiyoydm09