Предмет: Геометрия,
автор: truebeauty
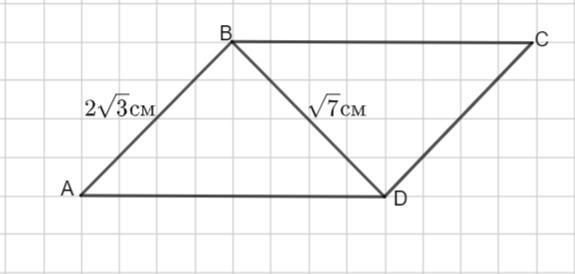
Дан параллелограмм ABCD. AB = 2квадратный корень3 см, BD =квадратный корень 7 см, ∠B = 150°. Найди длину стороны BC.
habibulinalera930:
Нешел?
Ты ответил?
Ответы
Автор ответа:
1
Ответ:
1 см или 5 см
Объяснение:
Пусть дан параллелограмм ABCD , ∠ B=150°
∠A и ∠B - внутренние односторонние, образованные BC║AD и секущей АВ. Тогда ∠A + ∠B =180°. Значит, ∠А=180°-150°=30°.
Рассмотрим треугольник ABD. Пусть AD=x см.
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Значит,
Значит, АD= 1 cм и АD= 5 cм.
Противолежащие стороны параллелограмма равны . Значит, ВС= АD=1 см или 5 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Acula79
Предмет: География,
автор: Violetta66661
Предмет: Английский язык,
автор: bayramovaaysel
Предмет: Математика,
автор: lelykirina
Предмет: Математика,
автор: vipkakunina