Предмет: Геометрия,
автор: dilnaz5993
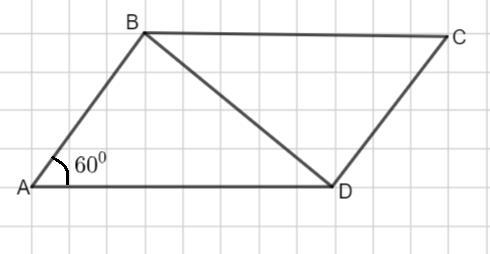
Дан параллелограмм ABCD. AB:BC= 3:4, BD=2√13см, угол А=60° . Найди длины сторон параллелограмма
Приложения:
Ответы
Автор ответа:
2
Ответ:
6 см и 8 см.
Объяснение:
Рассмотрим параллелограмм ABCD.
∠A=60°. Противолежащие стороны параллелограмма равны, то есть
BC=AD.
Пусть АВ = 3x см , AD=4x см.
Применим к треугольнику ABD теорему косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Так как сторона не может быть отрицательным числом, то х = 2 см.
Тогда АВ= 2*3=6 см, ВС= 2*4=8 см.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: muryasova81
Предмет: Химия,
автор: skovaliova18
Предмет: Русский язык,
автор: KACHEK705
Предмет: Биология,
автор: Sodirxona
Предмет: Математика,
автор: Tertu