Question

диагонали параллелограмма равны 4√2 и 6 см а угол между ними равен 45° найдите длины сторон ппараллелограмма
(онлайн мектеп, можно просто ответ)

Answer 1

Ответ:

$AB = CD = \sqrt{5}$ см.

$BC = AD = \sqrt{29}$ см.

Объяснение:

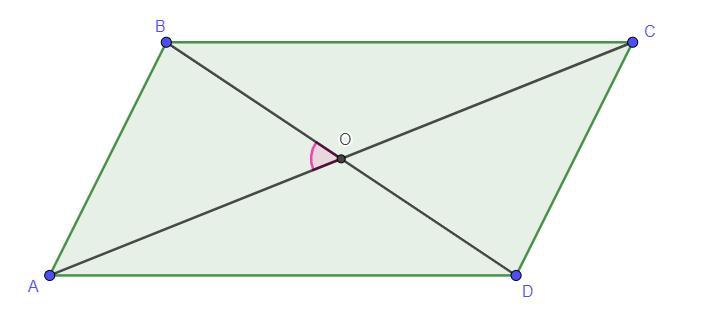
Дано: ABCD - параллелограмм, AC = 6 см, $BD= 4\sqrt{2}$ см, ∠AOB = 45°

Найти: AB,BC,CD,DA - ?

Решение: Так как по условию ABCD - параллелограмм, то по свойствам параллелограмма его противоположные стороны равны, тогда

AB = CD, AD = BC. По свойствам параллелограмма его диагонали точкой пересечения делятся пополам, тогда BO = OD = BD : 2 = $4\sqrt{2} : 2 =2\sqrt{2}$ см,

AO = OC = AC : 2 = 6 : 2 = 3 см. Рассмотрим треугольник ΔBOA.

По теореме косинусов:

$AB = \sqrt{AO^{2} + BO^{2} - 2AO * BO * \cos\angle BOA} = \sqrt{3^{2} + (2\sqrt{2} )^{2} - 2*3 * 2\sqrt{2} * \cos 45^{\circ}} =$

$=\sqrt{9 + 8 - 2 * 3 * 2\sqrt{2} *\frac{\sqrt{2} }{2} } = \sqrt{17 - 12} = \sqrt{5}$ см.

По тождеству параллелограмма:

$2AB^{2} + 2BC^{2} = AC^{2} + BD^{2} \Longrightarrow BC = \sqrt{\frac{AC^{2} + BD^{2} - 2AB^{2}} {2} } =$

$= \sqrt{\frac{6^{2} + (4\sqrt{2} )^{2} - 2 * (\sqrt{5} )^{2}}{2} } = \sqrt{\frac{36 + 32 - 10}{2} } = \sqrt{\frac{68 - 10}{2}} = \sqrt{\frac{58}{2} } = \sqrt{29}$ см.

$AB = CD = \sqrt{5}$ см.

$BC = AD = \sqrt{29}$ см.