Предмет: Алгебра,
автор: zavollgskay
Здравствуйте, помогите пожалуйста сделать, чтобы я хоть принцип действия понял, я то вообще не понимаю за что браться, пожалуйста, хоть несколько из примеров
НУЖНО ИЗ ФОРМУЛЫ ВЫРАЗИТЬ ПЕРЕМЕННУЮ
Приложения:
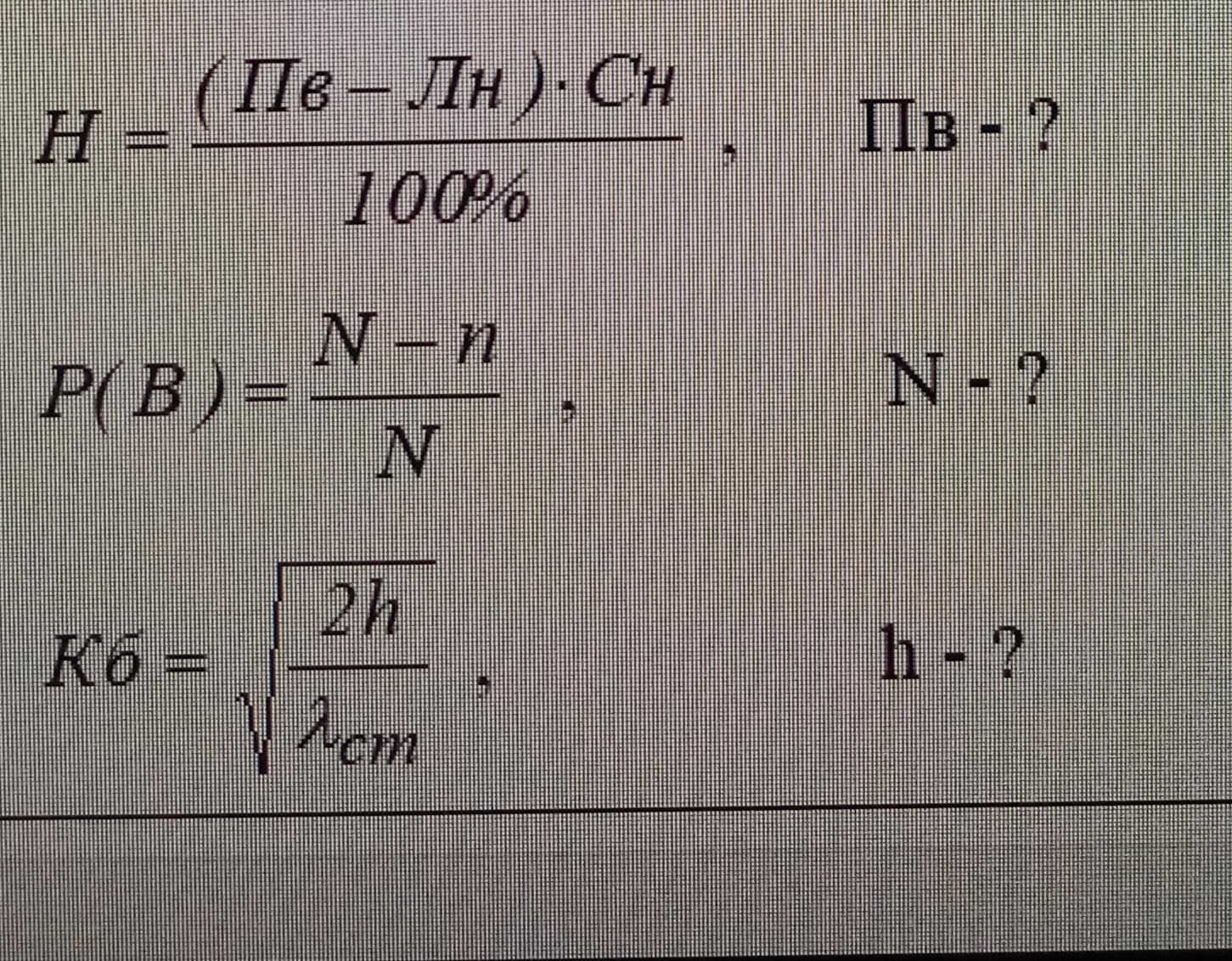

Ответы
Автор ответа:
1
(Так как в редакторе формул нет кириллицы, то написала буквы на латинице. Буква "П" заменена на "Р" , "в" - на "b" , "н" - на "n" .)
Автор ответа:
1
Объяснение:
1. Н=(Пв-Лн)*Сн/100%
Пв-Лн=Н*100%/Сн
Пв=Лн+Н*100%/Сн=(Лн*Сн+Н*100%)/Сн.
Похожие вопросы
Предмет: Математика,
автор: CoolArtyom
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: kiiiiiiiiiissa
Предмет: Алгебра,
автор: лидия91
Предмет: Химия,
автор: ilyadolgopolovowgpu3